题目内容
已知函数f(x)=
ax2-x+lnx(a∈R,a≠0)
(Ⅰ)当a=2时,求曲线y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若在区间[1,+∞)上函数f(x)的图象恒在直线y=ax下方,求a的取值范围.
| 1 |
| 2 |
(Ⅰ)当a=2时,求曲线y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若在区间[1,+∞)上函数f(x)的图象恒在直线y=ax下方,求a的取值范围.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)把a=2代入函数解析式,求出f(1)的值,求出原函数的导函数,得到f′(1)的值,然后由直线方程的点斜式求切线方程;
(Ⅱ)构造辅助函数g(x)=f(x)-ax,把在区间[1,+∞)上函数f(x)的图象恒在直线y=ax下方转化为
在[1,+∞)上g(x)max<0恒成立.求出函数g(x)的导函数,得到导函数的零点,由导函数的零点对定义域分段,然后对a分类讨论,由导数得到函数g(x)在各区间段内的最大值,由最大值小于0求解a的取值范围.
(Ⅱ)构造辅助函数g(x)=f(x)-ax,把在区间[1,+∞)上函数f(x)的图象恒在直线y=ax下方转化为
在[1,+∞)上g(x)max<0恒成立.求出函数g(x)的导函数,得到导函数的零点,由导函数的零点对定义域分段,然后对a分类讨论,由导数得到函数g(x)在各区间段内的最大值,由最大值小于0求解a的取值范围.
解答:
解:(Ⅰ)函数的定义域为(0,+∞).
当a=2时,f(x)=x2-x+lnx,f′(x)=2x-1+
.
∴f(1)=0,f′(1)=2.
∴曲线y=f(x)在(1,f(1))处的切线方程为y=2(x-1),
即2x-y-2=0;
(Ⅱ)令g(x)=f(x)-ax=
ax2-x+lnx-ax,定义域为(0,+∞),
在区间[1,+∞)上,函数f(x)的图象恒在直线y=ax下方,
等价于g(0)<0在[1,+∞)上恒成立.
∴只要在[1,+∞)上g(x)max<0恒成立.
∵g′(x)=ax-1+
-a=
,
由g′(x)=0,得x1=1,x2=
.
当0<a≤1时,x1=1≤x2=
,g(x)在(
,+∞)上单调递增,
并且在该区间上g(x)∈(g(x2),+∞),不可能有g(x)max<0,不合题意.
当a>1时,x2=
<x1=1,g(x)在(1,+∞)上单调递增,
并且在该区间上g(x)∈[g(1),+∞),不可能有g(x)max<0,不合题意.
当a<0时,x2=
<0,x1=1,g(x)在[1,+∞)上单调递减,
g(x)max=g(1)=
a-1+0-a<0,解得-2<a<0.
综上,a∈(-2,0)时,函数f(x)的图象恒在直线y=ax下方.
当a=2时,f(x)=x2-x+lnx,f′(x)=2x-1+
| 1 |
| x |
∴f(1)=0,f′(1)=2.
∴曲线y=f(x)在(1,f(1))处的切线方程为y=2(x-1),
即2x-y-2=0;
(Ⅱ)令g(x)=f(x)-ax=
| 1 |
| 2 |
在区间[1,+∞)上,函数f(x)的图象恒在直线y=ax下方,
等价于g(0)<0在[1,+∞)上恒成立.
∴只要在[1,+∞)上g(x)max<0恒成立.
∵g′(x)=ax-1+
| 1 |
| x |
| (ax-1)(x-1) |
| x |
由g′(x)=0,得x1=1,x2=
| 1 |
| a |
当0<a≤1时,x1=1≤x2=
| 1 |
| a |
| 1 |
| a |
并且在该区间上g(x)∈(g(x2),+∞),不可能有g(x)max<0,不合题意.
当a>1时,x2=
| 1 |
| a |
并且在该区间上g(x)∈[g(1),+∞),不可能有g(x)max<0,不合题意.
当a<0时,x2=
| 1 |
| a |
g(x)max=g(1)=
| 1 |
| 2 |
综上,a∈(-2,0)时,函数f(x)的图象恒在直线y=ax下方.
点评:本题考查利用导数研究曲线上某点处的切线方程,函数在曲线上某点处的导数,就是曲线过该点的切线的斜率,考查了利用导数求函数的最值,体现了数学转化思想方法和分类讨论的数学思想方法,属有一定难度题目.

练习册系列答案
相关题目
如果某物体的运动方程为s=2(1-t2)(s的单位为m,t的单位为s),那么其在1.2s末的瞬时速度为( )
| A、-4.8m/s |
| B、-2.8m/s |
| C、0.88 m/s |
| D、4.8 m/s |
对于任意x∈[-1,0],恒有
x3-x2-3x-2m≤3成立,则m的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、[-1,+∞) | ||
C、[-
| ||
| D、[-2,+∞) |
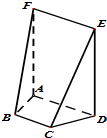 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=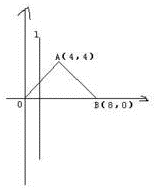 如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).
如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).