题目内容
已知数列{an}是首项为1,公差不为0的等差数列,且a1,a2,a5成等比数列
(1)求数列{an}的通项公式;
(2)若bn=
,Sn是数列{bn}的前n项和,求证:Sn<
.
(1)求数列{an}的通项公式;
(2)若bn=
| 1 |
| anan+1 |
| 1 |
| 2 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用裂项求和即可得出.
(2)利用裂项求和即可得出.
解答:
解:(1)设数列{an}公差为d,且d≠0,
∵a1,a2,a5成等比数列,a1=1
∴(1+d)2=1×(1+4d)
解得d=2,
∴an=2n-1.
(2)bn=
=
=
(
-
)
∴Sn=b1+b2+…+bn=
(1-
)+
(
-
)+…+
(
-
)=
(1-
)<
∵a1,a2,a5成等比数列,a1=1
∴(1+d)2=1×(1+4d)
解得d=2,
∴an=2n-1.
(2)bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
点评:熟练掌握等差数列与等比数列的通项公式、裂项求和是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点O在△ABC内,且2
+3
+6
=
,那么△OBC、△OCA、△OAB的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:2:3 |
| B、2:3:6 |
| C、3:2:1 |
| D、6:3:2 |
已知向量
=(x1,y1),
=(x2,y2),若|
|=2,|
|=3,
•
=-6,并且x2+y2≠0,则
的值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
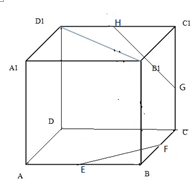 如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.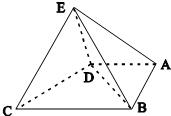 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.