题目内容
在各项均为正数的等比数列{an}中,
≤2,则下列结论中正确的是( )
| a3+a11 |
| a7 |
| A、数列{an}是常数列 |
| B、数列{an}是递增数列 |
| C、数列{an}是递减数列 |
| D、数列{an}有可能是递增数列也有可能是递减数列 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:设公比为q,则由
≤2可得 (q4-1)2≤0,求得q=1,从而得出结论.
| a3+a11 |
| a7 |
解答:
解:设公比为q,则由
≤2可得a3+a3q8≤2a3q4,即 (q4-1)2≤0,求得q=1,或q=-1(舍去),
故数列{an}是常数列,
故选:A.
| a3+a11 |
| a7 |
故数列{an}是常数列,
故选:A.
点评:本题主要考查等比数列的定义和性质,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
设集合A={1,3,4},B={2,3,6},则A∪B等于( )
| A、{3} |
| B、{1,2,3,4} |
| C、{1,2,3,6} |
| D、{1,2,3,4,6} |
已知点O在△ABC内,且2
+3
+6
=
,那么△OBC、△OCA、△OAB的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:2:3 |
| B、2:3:6 |
| C、3:2:1 |
| D、6:3:2 |
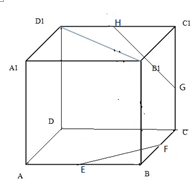 如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.