题目内容
过正棱台两底面中心的截面一定是( )
| A、直角梯形 | B、等腰梯形 |
| C、一般梯形或等腰梯形 | D、矩形 |
考点:棱台的结构特征
专题:空间位置关系与距离
分析:首先,分情况进行讨论:一是当截面过侧棱时,截面是一般梯形;二是当截面不过侧棱时,根据对称性,
然后得到结果.
然后得到结果.
解答:
解:当过正棱台两底面中心的截面与两底面的交线一定平行且不相等,
当截面过侧棱时,截面是一般梯形;
当截面不过侧棱时,根据对称性,
得截面与两底面的交线一定相等,
故截面是等腰梯形,
∴过正棱台两底面中心的截面一定是一般梯形或等腰梯形.
故选:C.
当截面过侧棱时,截面是一般梯形;
当截面不过侧棱时,根据对称性,
得截面与两底面的交线一定相等,
故截面是等腰梯形,
∴过正棱台两底面中心的截面一定是一般梯形或等腰梯形.
故选:C.
点评:本题重点考查了空间中截面和平面图形的关系、截面的性质、空间中线的位置关系等知识,考查空间想象能力,解题关键是准确理解空间图形和平面图形的区别.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
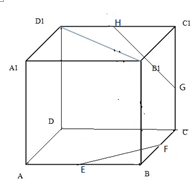 如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.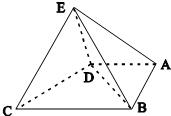 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.