题目内容
7.已知θ∈{α|α=kπ+(-1)k+1•$\frac{π}{4}$,k∈Z},则角θ的终边所在的象限是三,四.分析 对k分奇数与偶数讨论利用终边相同的角的集合的定义即可得出.
解答 解:当k=2n+1(n∈Z)时,α=(2n+1)π+$\frac{π}{4}$,角θ的终边在第三象限.
当k=2n(n∈Z)时,α=2nπ-$\frac{π}{4}$,角θ的终边在第四象限.
故答案为:三,四.
点评 本题考查了终边相同的角的集合、分类讨论的思想方法,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
17.已知函数f(x)=$\frac{1}{3}{x^3}$-x+c+1有两个不同零点,且有一个零点恰为f(x)的极小值点,则c的值为( )
| A. | 0 | B. | $-\frac{5}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{5}{3}$或$-\frac{1}{3}$ |
18.已知梯形ABCD中,AB⊥AD,$\overrightarrow{AB}=3\overrightarrow{DC},cos∠DAC=\frac{{\sqrt{3}}}{2},\overrightarrow{BE}=m\overrightarrow{BC}$(0<m<1),若|$\overrightarrow{AE}$|2=$|{\overrightarrow{AC}}||{\overrightarrow{AB}}$|,则$\frac{CE}{CB}$=( )
| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{2+\sqrt{15}}{7}$ |
15.△ABC中,a,b,c分别为角A,B,C的对边,a=$\sqrt{3}$,b=$\sqrt{2}$,B=45°,则角C的大小为( )
| A. | 15° | B. | 75° | C. | 15°或75° | D. | 60°或120° |
12.在复平面内,复数$\frac{2}{1+i}$(i为虚数单位)对应的点与原点的距离是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
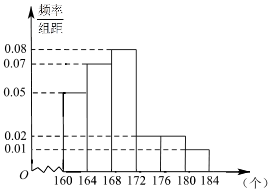 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.