题目内容
17.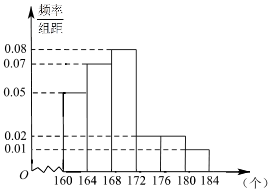 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.(1)试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上(含172个)的人数;
(2)在这50名市民中成绩在172个以上(含172个)的人中任意抽取2人,该2人中成绩排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若η~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974.
分析 (1)利用组中值代替本组数据计算平均值,和168比较得出结论;求出后3组的面积之和,再乘上总人数得出成绩在172个以上(含172个)的人数;
(2)利用正态分布得出全市前130名的成绩,得出50名社区居民中符合条件的人数,使用超几何分布的概率公式得出分布列.
解答 解:(1)该社区50名市民的平均成绩为162×0.05×4+166×0.07×4+170×0.08×4+174×0.02×4+178×0.02×4+182×0.01×4=168.72,
∴该社区被测试的50名市民的成绩略高于全市市民的平均成绩.
50名市民中成绩在172个以上(含172个)的人数为50×(0.02+0.02+0.01)×4=10.
(2)∵P(168-3×4≤ξ<168+3×4)=0.9974,∴P(ξ≥180)=$\frac{1}{2}$(1-0.9974)=0.0013,
∵0.0013×100 000=130.
∴全市前130名的成绩在180个以上(含180个),
这50人中成绩在180 个以上(含180个)的有2人.
∴随机变量ξ的可能取值为0,1,2,
∴P(ξ=0)=$\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$=$\frac{28}{45}$,P(ξ=1)=$\frac{{C}_{8}^{1}{•C}_{2}^{1}}{{C}_{10}^{2}}$=$\frac{16}{45}$,P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{1}{45}$,
∴E(ξ)=0×$\frac{28}{45}$+1×$\frac{16}{45}$+2×$\frac{1}{45}$=$\frac{2}{5}$.
点评 本题考查了频率分布直方图,正态分布与超几何分布,属于中档题.


| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
| A. | {1} | B. | {(1,3)} | C. | {(1,2)} | D. | {2} |