Question

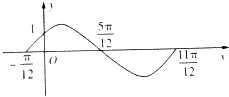函数f₁（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的一段图象如图所示，且函数过点（0，1）
（1）求函数f₁（x）的解析式；
（2）将函数y=f₁（x）的图象向右平移

π

4

个单位长度，得到函数y=f₂（x），求y=f₁（x）+f₂（x）的最大值，并求此时自变量x的集合．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的求值,三角函数的图像与性质

分析：（1）利用函数的图象求函数的解析式，主要确定函数的A，ω，φ的值．
（2）通过函数（1）的关系式求出f2(x)=2sin(2x-

π

3

)，进一步求出函数y的关系式，最后变换成正弦型函数解析式的形式，最后求得解的结果．

解答： 解：（1）根据函数的图象：T=

2π

ω

=

11π

12

+

1π

12

=π，
解得：ω=2．
当x=

5π

12

时，函数f1(

5π

12

)=0（|φ|＜

π

2

），
解得：φ=

π

6

．
函数的图象过（0，1），
则：f₁（0）=1，
即Asin

π

6

=1，
解得：A=2，
所以函数的解析式为：f1(x)=2sin(2x+

π

6

)．
（2）函数f1(x)=2sin(2x+

π

6

)向右平移

π

4

个单位，
得到：f2(x)=2sin(2(x-

π

4

)+

π

6

)=2sin(2x-

π

3

)，
则：y=f₁（x）+f₂（x）=2sin(2x+

π

6

)+2sin(2x-

π

3

)
=2sin(2x+

π

6

)-2cos(2x+

π

6

)
=2

2

sin(2x-

π

12

)，
当2x-

π

12

=2kπ+

π

2

（k∈Z）时，函数取最大值2

2

．
解得：x=kπ+

7π

24

（k∈Z）．
所以：当{x|x=kπ+

7π

24

}（k∈Z），函数取得最大值2

2

．

点评：本题考查的知识要点：利用函数的图象求函数的解析式，函数图象的变换问题，三角函数关系式的恒等变换，属于基础题型．