题目内容
已知点P是椭圆
+
=1上的动点，M为过P且垂直于x轴的直线上的点，
=λ．求点M的轨迹方程，并说明轨迹是什么曲线．
| x2 |
| 16 |
| y2 |
| 7 |
| |OP| |
| |OM| |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设M（x，y），根据条件列出关于λ的方程（16λ2-9）x2+16λ2y2=448，然后再分类讨论，即可得出结论．
解答：
解：设M（x，y），其中x∈[-4，4]．
由已知
=λ及点P在椭圆C上，可得
=λ2，
整理得（16λ2-9）x2+16λ2y2=112，其中x∈[-4，4]．
①λ=
时，化简得9y2=112．
所以点M的轨迹方程为y=±
（-4≤x≤4），轨迹是两条平行于x轴的线段．
②λ≠
时，方程变形为
+
=1，其中x∈[-4，4]；
当0＜λ＜
时，点M的轨迹为中心在原点、实轴在y轴上的双曲线满足-4≤x≤4的部分；
当
＜λ＜1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆满足-4≤x≤4的部分；
当λ≥1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆．
由已知
| |OP| |
| |OM| |
| 9x2+112 |
| 16(x2+y2) |
整理得（16λ2-9）x2+16λ2y2=112，其中x∈[-4，4]．
①λ=
| 3 |
| 4 |
所以点M的轨迹方程为y=±
4
| ||
| 3 |
②λ≠
| 3 |
| 4 |
| x2 | ||
|
| y2 | ||
|
当0＜λ＜
| 3 |
| 4 |
当
| 3 |
| 4 |
当λ≥1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆．
点评：本题主要考查圆锥曲线的定义和性质及其方程．考查分类讨论思想，是中档题．
练习册系列答案
相关题目
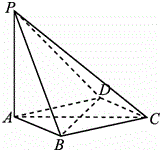如图，在四棱椎P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．
如图程序框图表示求