题目内容
已知函数f(x)=
.
(I)求函数f(x)的单调区间;
(Ⅱ)是否存在实数m,使不等式
ln2>mln(x+1)在-1<x<0时恒成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
(Ⅲ)已知正整数列{cn}中,(Cn)(n+1)2=e
(n∈N*),求数列{cn}中的最大项.
| 1 |
| (x+1)ln(x+1) |
(I)求函数f(x)的单调区间;
(Ⅱ)是否存在实数m,使不等式
| 1 |
| x+1 |
(Ⅲ)已知正整数列{cn}中,(Cn)(n+1)2=e
| 1 |
| f(n) |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)确定函数的定义域然后求导数fˊ(x),根据导数和函数的单调性的关系,求得函数的单调区间.
(Ⅱ)恒成立的问题,分离参数,只需m>
在-1<x<0时恒成立.求出
最大值即可.
(Ⅲ)先化简得到(Cn)n+1=n+1,然后构造函数,结合导数判断该函数在[2,+∞)内的单调性,进而可知{cn}的单调性,即可判断.
(Ⅱ)恒成立的问题,分离参数,只需m>
| ln2 |
| (x+1)ln(x+1) |
| ln2 |
| (x+1)ln(x+1) |
(Ⅲ)先化简得到(Cn)n+1=n+1,然后构造函数,结合导数判断该函数在[2,+∞)内的单调性,进而可知{cn}的单调性,即可判断.
解答:
解:(Ⅰ)根据函数解析式得,
解得x>-1且x≠0.
∴函数f(x)的定义域是{x|x∈R,x>-1且x≠0}.
∵f(x)=
.
∴f′(x)=-
,
由f'(x)>0得ln(x+1)+1<0.∴-1<x<e-1-1.
∴函数f(x)的增区间为(-1,e-1-1).
由f'(x)<0得ln(x+1)+1>0.∴x>e-1-1.
∴函数f(x)的减区间为(e-1-1,+∞).
(Ⅱ)∵e-1-1<x<0,∴e-1<x+1<1.
∴-1<ln(x+1)<0.∴ln(x+1)+1>0
当e-1-1<x<0时,f′(x)=-
<0,
∴函数f(x)在区间(e-1-1,0)上为减函数,
由(1)可知函数f(x)在区间(-1,e-1-1)上为增函数.
当x=e-1-1时,f(x)取得最大值.∴[f(x)]最大=f(e-1-1)=-e.
∵
ln2>mln(x+1)在-1<x<0时恒成立.
∴m>
在-1<x<0时恒成立.
∵
在-1<x<0时的最大值等于-eln2.
∴m>-eln2.
∴当m>-eln2时,不等式
ln2>mln(x+1)在-1<x<0时恒成立.
(Ⅲ)由已知(Cn)(n+1)2=e
=e(n+1)ln(n+1)=(eln(n+1))n+1=(n+1)n+1,
∴(Cn)n+1=n+1,
即lnCn=
,
令g(x)=
,
∴g′(x)=
,
当x≥2时,ln(x+1)>1,即f′(x)<0,
∴函数g(x)在[2,+∞)为单调减函数,
由lnCn=
,
∴n≥2 时,{lncn}是递减数列.即{cn}是递减数列.
又c12=2,∴c1=
,
c23=3,∴c2=
,
∵c1<c2,
∴数列{cn}中的最大项为c2=
,
|
∴函数f(x)的定义域是{x|x∈R,x>-1且x≠0}.
∵f(x)=
| 1 |
| (x+1)ln(x+1) |
∴f′(x)=-
| ln(x+1)+1 |
| (x+1)2ln2(x+1) |
由f'(x)>0得ln(x+1)+1<0.∴-1<x<e-1-1.
∴函数f(x)的增区间为(-1,e-1-1).
由f'(x)<0得ln(x+1)+1>0.∴x>e-1-1.
∴函数f(x)的减区间为(e-1-1,+∞).
(Ⅱ)∵e-1-1<x<0,∴e-1<x+1<1.
∴-1<ln(x+1)<0.∴ln(x+1)+1>0
当e-1-1<x<0时,f′(x)=-
| ln(x+1)+1 |
| (x+1)2ln2(x+1) |
∴函数f(x)在区间(e-1-1,0)上为减函数,
由(1)可知函数f(x)在区间(-1,e-1-1)上为增函数.
当x=e-1-1时,f(x)取得最大值.∴[f(x)]最大=f(e-1-1)=-e.
∵
| 1 |
| x+1 |
∴m>
| ln2 |
| (x+1)ln(x+1) |
∵
| ln2 |
| (x+1)ln(x+1) |
∴m>-eln2.
∴当m>-eln2时,不等式
| 1 |
| x+1 |
(Ⅲ)由已知(Cn)(n+1)2=e
| 1 |
| f(n) |
∴(Cn)n+1=n+1,
即lnCn=
| ln(n+1) |
| n+1 |
令g(x)=
| ln(x+1) |
| x+1 |
∴g′(x)=
| 1-ln(x+1) |
| (x+1)2 |
当x≥2时,ln(x+1)>1,即f′(x)<0,
∴函数g(x)在[2,+∞)为单调减函数,
由lnCn=
| ln(n+1) |
| n+1 |
∴n≥2 时,{lncn}是递减数列.即{cn}是递减数列.
又c12=2,∴c1=
| 2 |
c23=3,∴c2=
| 3 | 3 |
∵c1<c2,
∴数列{cn}中的最大项为c2=
| 3 | 3 |
点评:本小题主要考查函数与导数等知识,利用函数的单调性判断相应数列的单调性及利用单调性判断数列取得的最大项.考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力.属于难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 淮北市某小区为了解居民对“小区物业管理”的满意度,现随机抽取
淮北市某小区为了解居民对“小区物业管理”的满意度,现随机抽取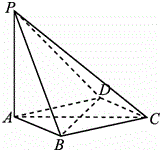 如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°. 如图程序框图表示求
如图程序框图表示求