题目内容
3.在平面直角坐标系xOy中,已知点$P({\frac{1}{2},\frac{{\sqrt{3}}}{2}})$,将向量$\overrightarrow{OP}$绕原点O按逆时针方向旋转x弧度得到向量$\overrightarrow{OQ}$.(1)若$x=\frac{π}{4}$,求点Q的坐标;
(2)已知函数f(x)=$\overrightarrow{OP}$•$\overrightarrow{OQ}$,令$g(x)=f(x)•f({x+\frac{π}{3}})$,求函数g(x)的值域.
分析 (1)P点坐标化为(cos$\frac{π}{3}$,sin$\frac{π}{3}$),故Q点坐标(cos($\frac{π}{3}+\frac{π}{4}$),sin($\frac{π}{3}+\frac{π}{4}$)),利用和角公式计算即可;
(2)用三角恒等变换化简f(x)的解析式,得出g(x)的解析式,根据正弦函数的性质得出g(x)的值域.
解答 解:(1)P((cos$\frac{π}{3}$,sin$\frac{π}{3}$),
cos($\frac{π}{3}+\frac{π}{4}$)=$\frac{1}{2}×\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}-\sqrt{6}}{4}$,
sin($\frac{π}{3}+\frac{π}{4}$)=$\frac{\sqrt{3}}{2}×\frac{\sqrt{2}}{2}$+$\frac{1}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$,
∴点Q的坐标为$({\frac{{\sqrt{2}-\sqrt{6}}}{4},\frac{{\sqrt{2}+\sqrt{6}}}{4}})$.
(2)f(x)=$\frac{1}{2}$cos($\frac{π}{3}$+x)+$\frac{\sqrt{3}}{2}$sin($\frac{π}{3}$+x)=$\frac{1}{4}cosx-\frac{{\sqrt{3}}}{4}sinx+\frac{3}{4}cosx+\frac{{\sqrt{3}}}{4}sinx=cosx$,
∴g(x)=cosx•cos(x+$\frac{π}{3}$)=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sinxcosx=$\frac{1+cos2x}{4}$-$\frac{\sqrt{3}}{4}$sin2x=$\frac{1}{4}$-$\frac{1}{2}$sin(2x-$\frac{π}{6}$).
因$-1≤sin({2x-\frac{π}{6}})≤1$,故g(x)的值域为$[{-\frac{1}{4},\frac{3}{4}}]$.
点评 本题考查了平面向量的数量积运算,三角恒等变换,正弦函数的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案| 身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重y(kg) | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{(1)}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{(2)}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于1kg的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | $a>2\sqrt{2}$ | B. | $2\sqrt{2}<a<3$ | C. | a>3 | D. | $3<a<2\sqrt{3}$ |
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$i | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{2}$i |
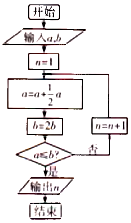 《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )
《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )