题目内容
抛物线y2=4x上与焦点距离等于4的点的坐标是 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x的值，代入抛物线方程求得y值，即可得到所求点的坐标．
解答：
解：∵抛物线方程为y2=4x，
∴焦点为F（1，0），准线为l：x=-1
∵抛物线y2=4x上一点P到焦点的距离等于4，
∴根据抛物线定义可知P到准线的距离等于4，
即x+1=4，解之得x=3，
代入抛物线方程求得y=±2
，
故答案为：（3，±2
）
∴焦点为F（1，0），准线为l：x=-1
∵抛物线y2=4x上一点P到焦点的距离等于4，
∴根据抛物线定义可知P到准线的距离等于4，
即x+1=4，解之得x=3，
代入抛物线方程求得y=±2
| 3 |
故答案为：（3，±2
| 3 |
点评：本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决．
练习册系列答案
相关题目
已知过点A（2，m）和B（m，5）的直线与直线2x-y+1=0平行，则m的值为（ ）
| A、0 | B、1 | C、2 | D、3 |
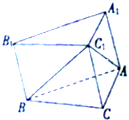如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |