题目内容
2.已知f(x)=$\frac{3}{k}$sin$\frac{π(x-2k+2)}{2}$,x∈[2(k-1),2k],其中k∈N*,令g(x)=f(x)-|lnx|,则g(x)的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由f(x)的表达式,先求出函数在[0,6]上的解析式和图象,由g(x)=f(x)-|lnx|=0得f(x)=|lnx|,然后作出两个函数的图象,利用数形结合判断交点个数进行求解即可.
解答  解:f(x)=$\frac{3}{k}$sin$\frac{π(x-2k+2)}{2}$=$\frac{3}{k}$sin($\frac{π}{2}$x+(1-k)π),
解:f(x)=$\frac{3}{k}$sin$\frac{π(x-2k+2)}{2}$=$\frac{3}{k}$sin($\frac{π}{2}$x+(1-k)π),
若k=1,则f(x)=3sin$\frac{π}{2}$x,x∈[0,2],
若k=2,则f(x)=$\frac{3}{2}$sin($\frac{π}{2}$x-π)=-$\frac{3}{2}$sin$\frac{π}{2}$x,x∈[2,4],
若k=3,则f(x)=sin($\frac{π}{2}$x-2π)=sin$\frac{π}{2}$x,x∈[4,6],
由g(x)=f(x)-|lnx|=0得f(x)=|lnx|,
作出函数f(x)与y=|lnx|在[0,6]上的图象,
当k≥3时,f(x)≤1,
由图象可知两个函数有4个交点,即函数g(x)的零点个数为4个,
故选:D.
点评 本题主要考查函数零点个数的判断,利用函数与方程之间的关系,转化为两个函数的交点个数问题,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
12.已知函数y=f(x)的定义域为R,对任意的实数x都满足f(x+2)=f(x),当x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=|lgx|的图象的交点共有( )
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 2个 |
13.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
10.已知集合M={x|$\frac{1}{x}$≤1},N={x|x2-x-6<0},则M∩N为( )
| A. | {x|-2≤x<0或1<x≤3} | B. | {x|-2<x<0或1≤x<3} | C. | {x|x≤-2或x>3} | D. | {x|x<-2或x≥3} |
7.若曲线y=$\frac{1}{3}$x3+ax2+x存在垂直于y轴的切线,则实数a的取值范围为( )
| A. | (-∞,-$\frac{1}{2}$]∪[1,+∞) | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,-1]∪[0,+∞) | D. | [$\frac{1}{2}$,+∞) |
14.已知平面α和平面β相交,a是α内一条直线,则有( )
| A. | 在β内必存在与a平行的直线 | B. | 在β内必存在与a垂直的直线 | ||
| C. | 在β内不存在与a平行的直线 | D. | 在β内不一定存在与a垂直的直线 |
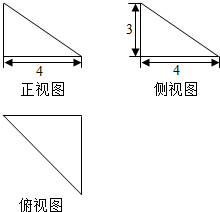 如图为一个几何体的三视图
如图为一个几何体的三视图