题目内容
13．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | 3 | B． | 6 | C． | 9 | D． | 12 |
分析 由三视图得该几何体是一个倒放的四棱锥S-ABCD，其中ABCD是矩形，AD=2，AB=3，SA⊥平面ABCD，且SA=3，由此能求出该几何体的体积．
解答 解：如图，由三视图得该几何体是一个倒放的四棱锥S-ABCD，
其中ABCD是矩形，AD=2，AB=3，SA⊥平面ABCD，且SA=3，
∴该几何体的体积为：
V=$\frac{1}{3}{S}_{矩形ABCD}×SA$=$\frac{1}{3}×2×3×3$=6．
故选：B．
点评 本题考查几何体的体积的求法，是基础题，解题时要认真审题，注意三视图的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．给定下列四个命题，其中为真命题的是（ ）
| A． | 若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行 | |
| B． | 若一个平面经过另一个平面的垂线，那么这两个平面相互垂直 | |
| C． | 垂直于同一直线的两条直线相互平行 | |
| D． | 若两个平面垂直，那么，一个平面内与它们的交线不垂直的直线一定垂直于另一个平面 |
4．${2^{1+{{log}_2}5}}$的值等于（ ）
| A． | $2+\sqrt{5}$ | B． | 10 | C． | $2+\frac{{\sqrt{2}}}{2}$ | D． | $1+\frac{{\sqrt{5}}}{2}$ |
8．f（x）=ax3+3x2+2，若f′（-1）=3，则函数在x=-1处的切线方程为（ ）
| A． | y=3x+5 | B． | y=3x-5 | C． | y=-3x+5 | D． | y=-3x-5 |
如图，已知正方体ABCD-A1B1C1D1
5．已知全集U=R，集合A={x|2＜x＜4}，B={x|-2≤x≤3}，则A∩（∁RB）等于（ ）
| A． | （1，2） | B． | （3，4） | C． | （1，3） | D． | （1，2）∪（3，4） |
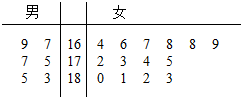某航空公司在2015年年初招收了20名空乘人员（服务员与空警），其中“男性空乘人员”5名，“女性空乘人员”14名，并对他们的身高进行了测量，其身高（单位：cm）的茎叶图如图所示．