题目内容
6.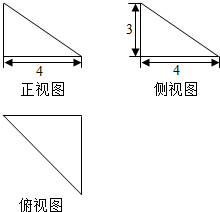 如图为一个几何体的三视图
如图为一个几何体的三视图(1)画出该几何体的直观.
(2)求该几何体的体积.
(3)求该几何体的表面积.
分析 (1)由几何体的三视图能作出几何体的直观图为一个三棱椎.
(2)先求出S△BCD,由此能求出该几何体的体积.
(3)该几何体的表面积S=S△ABC+S△ABD+S△ACD,由此能求出结果.
解答 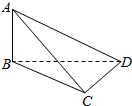 (本题满分12分)
(本题满分12分)
解:(1)由几何体的三视图得到几何体的直观图为一个三棱椎A-BCD,如右图,
其中AB⊥平面BCD,BC⊥CD,BD=CD=4,AB=3.
(2)由(1)知S△BCD=$\frac{1}{2}×{4}^{2}$=8,
∴该几何体的体积V=$\frac{1}{3}×{S}_{△BCD}×AB$=$\frac{1}{3}×8×3$=8.
(3)该几何体的表面积:
S=S△ABC+S△ABD+S△ACD
=$\frac{1}{2}×3×4\sqrt{2}+\frac{1}{2}×3×4+\frac{1}{2}×4×4+\frac{1}{2}×4×5$
=6$\sqrt{2}$+24.
点评 本题考查几何体的直观图的作法,考查几何体的体积、表面积的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
2.已知f(x)=$\frac{3}{k}$sin$\frac{π(x-2k+2)}{2}$,x∈[2(k-1),2k],其中k∈N*,令g(x)=f(x)-|lnx|,则g(x)的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知集合P={x|1<2x<2},Q={x|log${\;}_{\frac{1}{2}}$x>1},则P∩Q=( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2},1$) | C. | (-1,$\frac{1}{2}$) | D. | (0,1) |
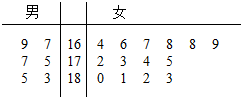 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”5名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.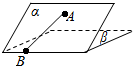 如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.
如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.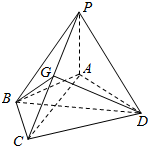 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°