题目内容
14．已知平面α和平面β相交，a是α内一条直线，则有（ ）| A． | 在β内必存在与a平行的直线 | B． | 在β内必存在与a垂直的直线 | ||
| C． | 在β内不存在与a平行的直线 | D． | 在β内不一定存在与a垂直的直线 |
分析 当a与平面α和平面β的交线相交时，在β内不存在与a平行的直线，当a与平面α和平面β的交线平行时，在β内存在与a平行的直线；由线面垂直的性质定理得在β内必存在与a垂直的直线．
解答 解：平面α和平面β相交，a是α内一条直线，
在A中：当a与平面α和平面β的交线相交时，在β内不存在与a平行的直线，故A错误；
在B中：平面α和平面β相交，a是α内一条直线，由线面垂直的性质定理得在β内必存在与a垂直的直线，故B正确；
在C中：当a与平面α和平面β的交线平行时，在β内存在与a平行的直线，故C错误；
在D中：由线面垂直的性质定理得在β内必存在与a垂直的直线，故D错误．
故选：B．
点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
相关题目
4．${2^{1+{{log}_2}5}}$的值等于（ ）
| A． | $2+\sqrt{5}$ | B． | 10 | C． | $2+\frac{{\sqrt{2}}}{2}$ | D． | $1+\frac{{\sqrt{5}}}{2}$ |
5．已知全集U=R，集合A={x|2＜x＜4}，B={x|-2≤x≤3}，则A∩（∁RB）等于（ ）
| A． | （1，2） | B． | （3，4） | C． | （1，3） | D． | （1，2）∪（3，4） |
2．已知f（x）=$\frac{3}{k}$sin$\frac{π（x-2k+2）}{2}$，x∈[2（k-1），2k]，其中k∈N*，令g（x）=f（x）-|lnx|，则g（x）的零点个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
6．已知点A（1，0）和B（1，2）是圆x2+y2-2x-2y+1=0上的两点，若在直线y=kx-1上存在点P，使得$\overrightarrow{PA}$$•\overrightarrow{PB}$=0，则k的取值范围是（ ）
| A． | k≥1 | B． | k≥$\frac{3}{4}$ | C． | k≤1 | D． | k≤$\frac{3}{4}$ |
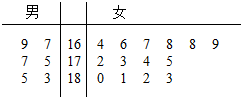某航空公司在2015年年初招收了20名空乘人员（服务员与空警），其中“男性空乘人员”5名，“女性空乘人员”14名，并对他们的身高进行了测量，其身高（单位：cm）的茎叶图如图所示．