题目内容
13.下列方案中,有可能拼接成一个四棱柱的是( )| A. | 两个三棱锥 | |
| B. | 一个三棱柱和一个三棱锥 | |
| C. | 一个三棱柱、一个四棱锥和一个三棱锥 | |
| D. | 一个四棱台和一个三棱柱 |
分析 根据题意,画出图形,得出四棱柱可以分成一个三棱柱,一个四棱锥和一个三棱锥,即得出C命题正确.
解答  解:如图所示,
解:如图所示,
四棱柱ABCD-A′B′C′D′,可以分成三棱柱AA′B′-DD′C′,
四棱锥C′-ABCD和三棱锥C′-ABB′,
即一个三棱柱、一个四棱锥和一个三棱锥能拼接成一个四棱柱.
故选:C.
点评 本题考查了空间几何体结构特征的应用问题,也考查了数形结合的应用问题,是基础题目.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3.在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a,E为侧棱PC的中点,又作DF⊥PB交PB于点F,则PB与平面EFD所成角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
8.若a>b>0,则下列不等式正确的是( )
| A. | $\frac{2ab}{a+b}$<$\frac{a+b}{2}$<$\sqrt{ab}$ | B. | $\sqrt{ab}$≤$\frac{2ab}{a+b}$≤$\frac{a+b}{2}$ | C. | $\frac{2ab}{a+b}$<$\sqrt{ab}$<$\frac{a+b}{2}$ | D. | $\sqrt{ab}$<$\frac{2ab}{a+b}$<$\frac{a+b}{2}$ |
20.下列各组中的两个函数是相等函数的是( )
| A. | y=x与y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2-1与y=|x|-1 | C. | y=x2与y=$\root{3}{{x}^{6}}$ | D. | y=$\root{3}{{x}^{3}}与y=\sqrt{{x}^{2}}$ |
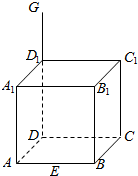 如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线. 如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.