题目内容
3．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的离心率为$\sqrt{2}$，则其渐近线方程为（ ）| A． | y=±x | B． | $y=±\sqrt{2}x$ | C． | $y=±\frac{{\sqrt{2}}}{2}x$ | D． | $y=±\frac{1}{2}x$ |
分析 由双曲线的离心率为$\sqrt{2}$，求出a=b，由此能求出比曲线的渐近线方程．
解答 解：∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的离心率为$\sqrt{2}$，
∴$\frac{c}{a}=\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\sqrt{2}$，
解得a=b，
∴该双曲线渐近线方程为y=±x．
故选：A．
点评 本题考查双曲线渐近线方程的求法，是基础题，解题时要认真审题，注意双曲线简单性质的合理运用．
练习册系列答案
相关题目
18．在平行四边形ABCD中，已知C（-3，0），D（3，0），点E，F满足$\overrightarrow{AC}=3\overrightarrow{AE}$，$\overrightarrow{DF}=2\overrightarrow{FA}$，且$|\overrightarrow{CF}|-|\overrightarrow{DE}|=4$，则点A的轨迹方程是（ ）
| A． | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | B． | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1（x≥2） | C． | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | D． | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}$=1（x≥3） |
8．设f（x）是定义在R上的增函数，且对任意x，都有f（-x）+f（x）=0恒成立，如果实数m，n满足不等式f（m2-6m+21）+f（n2-8n）＜0，那么m2+n2的取值范围是（ ）
| A． | （9，49） | B． | （13，49） | C． | （9，25） | D． | （3，7） |
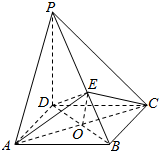如图所示，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，AB=2，PD=$\sqrt{6}$．O为AC与BD的交点，E为棱PB上一点
12．若动圆C过定点A（4，0），且在y轴上截得弦MN的长为8，则动圆圆心C的轨迹方程是（ ）
| A． | x2=8y | B． | x2=8y（x≠0） | C． | y2=8x | D． | y2=8x（x≠0） |