题目内容
4.已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,点C在∠AOB内,且∠AOC=60°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则$\frac{m}{n}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据题意,建立平面直角坐标系,用坐标表示向量,利用∠AOC=30°,即可求得结论
解答 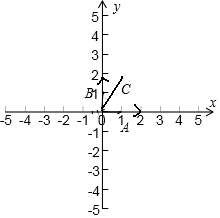 解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
建立如图所示的平面直角坐标系:
则$\overrightarrow{OA}$=(2,0),$\overrightarrow{OB}$=(0,$\sqrt{3}$),∵$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,
∴$\overrightarrow{OC}$=(2m,$\sqrt{3}$n),
∵∠AOC=60°,∴tan60°=$\frac{\sqrt{3}n}{2m}$=$\sqrt{3}$
∴$\frac{m}{n}$=$\frac{1}{2}$;
故选:A.
点评 本题考查向量知识的运用,考查向量的坐标运算,考查学生的计算能力,关键是正确建系,利用坐标法解答;属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
12.复平面上平行四边形ABCD的四个顶点中,A、B、C所对应的复数分别为2-3i、-2-3i、-3+2i,则D点对应的复数是( )
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
19.为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽取8位,他们的数学、物理、化学分数(折算成百分制)事实上对应如表:
(1)若规定80分以上为优秀,请填写如下2×2列联表,问是否有90%的把握认为是否优秀与科目有关;
(2)用变量y与x,z与x的相关系数说明物理与数学、化学与数学的相关程度;
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
| 优秀 | 不优秀 | 合计 | |
| 数学 | |||
| 物理 | |||
| 合计 |
(3)求y与x,z与x的线性回归方程(系数精确到0,01),当某位同学的数学成绩为50分时,估计其物理、化学两科的成绩.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}•\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,
回归直线方程是:$\widehat{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$,
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\overline{z}$=81,$\sum_{i=1}^{8}$(xi-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(yi-$\overline{y}$)2≈456,$\sum_{i=1}^{8}$(zi-$\overline{z}$)2≈550,≈688,$\sum_{i=1}^{8}$(xi-$\overline{x}$)(zi-$\overline{z}$)≈755,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
9.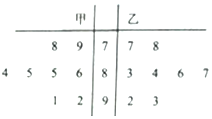 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
14.定义A-B={x|x∈A且x∉B}.已知A={1,2},B={1,3,4},则A-B=( )
| A. | {1} | B. | {2} | C. | {3,4} | D. | {1,2,3,4} |
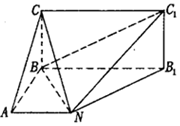 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1. 已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.
已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.