题目内容
16.已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$)的图象关于直线x=$\frac{π}{6}$对称,且图象上相邻最高点的距离为π.(1)求f(x)的解析式;
(2)将y=f(x)的图象向右平移$\frac{π}{6}$个单位,得到g(x)的图象若关于x的方程g(x)-(2m+1)=0在$[0,\frac{π}{2}]$上有唯一解,求实数m的取值范围.
分析 (1)由题意利用正弦函数的周期性以及图象的对称性,求得f(x)的解析式.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,根据题意,g(x)的图象和直线y=2m+1在[0 $\frac{π}{2}$]上只有一个交点,结合g(x)在$[0,\frac{π}{2}]$上的图象,求得m的范围.
解答 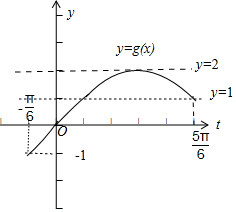 解:(1)因为f(x)的图象上相邻最高点的距离为$\frac{2π}{ω}$=π,
解:(1)因为f(x)的图象上相邻最高点的距离为$\frac{2π}{ω}$=π,
∴ω=2.
又f(x)的图象关于直线x=$\frac{π}{6}$对称,
∴2•$\frac{π}{6}$+φ=kπ+$\frac{π}{2}$,k∈Z,∵-$\frac{π}{2}$≤φ<$\frac{π}{2}$,∴φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)将y=f(x)的图象向右平移$\frac{π}{6}$个单位,
得到g(x)=2sin(2x-$\frac{π}{6}$)的图象,
根据方程g(x)-(2m+1)=0在$[0,\frac{π}{2}]$上有唯一解,
可得g(x)的图象和直线y=2m+1在[0 $\frac{π}{2}$]上只有一个交点,
在$[0,\frac{π}{2}]$上,2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],令t=2x-$\frac{π}{6}$,
则y=2sint在t∈[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象和直线y=2m+1只有一个交点,
只需-1≤2m+1<1或2m+1=2,解得-1≤m<0或m=$\frac{1}{2}$.
即实m的取值范围为{m|-1≤m<0或m=$\frac{1}{2}$}.
点评 本题主要考查正弦函数的周期性以及图象的对称性,函数y=Asin(ωx+φ)的图象变换规律,方程根的存在性以及个数判断,属于中档题.

| A. | 若a>b,c>d,则ac>bd | B. | 若ac>bc,则a>b | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若$\frac{a}{{c}^{2}}$<$\frac{b}{{c}^{2}}$,则a<b |
| A. | 科学家利用鱼的沉浮原理制造潜艇 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | $y=sin(\frac{x}{2}+\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=tan(x+\frac{π}{6})$ |
| A. | (-$\frac{1}{2}$,1] | B. | (-$\frac{1}{2}$,1) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,$\frac{1}{2}$] |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$+$\sqrt{3}$ | D. | $\frac{1}{2}$+$\sqrt{3}$ |
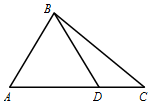 在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,线段AC上点D满足AD=2DC.
在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7}$,线段AC上点D满足AD=2DC.