题目内容

14．已知直线L与直线2x-y-5=0的倾斜角相等，且直线过点A（3，2）则直线L的方程2x-y-4=0．

分析 求出直线的斜率，利用点斜式取款机直线方程即可．

解答 解：直线L与直线2x-y-5=0的倾斜角相等，可得直线的斜率为：2，
直线过点A（3，2）则直线L的方程：y-2=2（x-3），解得2x-y-4=0．
故答案为：2x-y-4=0．

点评 本题考查直线方程的求法，考查计算能力．

练习册系列答案
相关题目
4．已知$sinθ=\frac{4}{5}$，$cosθ=-\frac{3}{5}$，则θ是（　　）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
5．已知函数f（x）=ex-1，g（x）=-（x-2）2+m，若存在a，b∈[0，3]，使得f（a）＞g（b）成立，求m的取值范围．
2．已知关于x的方程kx2+$\frac{1}{2}$kx+k-2=0有两个实根，其中一根在（0，1）之间，求实数k的取值范围．
9．若$\overrightarrow{OA}$=（3，2），$\overrightarrow{OB}$=（-4，y），并且$\overrightarrow{OB}$⊥$\overrightarrow{OA}$，则|$\overrightarrow{OB}$|=（　　）
A．$\sqrt{13}$B．4$\sqrt{13}$C．2$\sqrt{13}$D．2$\sqrt{11}$
19．已知数列{an}满足an+1=5an-6an-1（n≥2），且a1=1，a2=4，求数列{an}的通项公式．
6．已知数列{an}中，a1=$\frac{1}{2}$，Sn为数列|an|的前n项和，且Sn与$\frac{1}{{a}_{n}}$的一个等比中项为n（n∈N*），求{an}的通项公式．
3．在平面直角坐标系xOy中，已知点P（2，3），C（5，6），若在以点C为圆心，r为半径的圆上存在不同的两点A，B，使得$\overrightarrow{PA}$-2$\overrightarrow{AB}$=$\overrightarrow{0}$，则r的取值范围为[$\frac{3}{5}$$\sqrt{2}$，3$\sqrt{2}$）．
4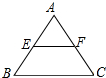．在三角形ABC中，E、F分别是AB、AC的中点，若在三角形内部，随机取一点Q，则点Q取自△AEF内部的概率是（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网