题目内容
 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;
(2)求异面直线EC与AB所成角的余弦值.
考点:异面直线及其所成的角,直线与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)应用面面垂直的性质定理,再由线面垂直的性质定理和判定定理,即可得证;
(2)分别取BC、AC、AE的中点F、H、G,连结HF、HG、FG,应用中位线定理,即可得到∠GHF为异面直线EC与AB所成角或其补角,再由余弦定理,即可得到所求值.
(2)分别取BC、AC、AE的中点F、H、G,连结HF、HG、FG,应用中位线定理,即可得到∠GHF为异面直线EC与AB所成角或其补角,再由余弦定理,即可得到所求值.
解答:
 (1)证明:由正方形ACDE所在的平面与平面ABC垂直,
(1)证明:由正方形ACDE所在的平面与平面ABC垂直,
面ABC∩面ACDE=AC,AC⊥BC,
则BC⊥面ACDE,
由AM?面ACDE,则AM⊥BC,
又正方形ACDE,则AM⊥EC,
则AM⊥平面EBC;
(2)解:分别取BC、AC、AE的中点F、H、G,连结HF、HG、FG,
则HG∥EC,HG=
EC,HF∥AB,HF=
AB,
即有∠GHF为异面直线EC与AB所成角或其补角,
令AC=1,则HF=
,GH=
,又在直角△GCF中CF=
,
GC=
=
,则GF=
,
则cos∠GHF=
=-
.
故异面直线EC与AB所成角斜弦值为
.
 (1)证明:由正方形ACDE所在的平面与平面ABC垂直,
(1)证明:由正方形ACDE所在的平面与平面ABC垂直,面ABC∩面ACDE=AC,AC⊥BC,
则BC⊥面ACDE,
由AM?面ACDE,则AM⊥BC,
又正方形ACDE,则AM⊥EC,
则AM⊥平面EBC;
(2)解:分别取BC、AC、AE的中点F、H、G,连结HF、HG、FG,
则HG∥EC,HG=
| 1 |
| 2 |
| 1 |
| 2 |
即有∠GHF为异面直线EC与AB所成角或其补角,
令AC=1,则HF=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
GC=
1+
|
| ||
| 2 |
| ||
| 2 |
则cos∠GHF=
| ||||||||
2•
|
| 1 |
| 2 |
故异面直线EC与AB所成角斜弦值为
| 1 |
| 2 |
点评:本题考查线面垂直和面面垂直的判定和性质定理及应用,考查异面直线所成角的求法,考查运算能力,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知F1、F2椭圆
+
=1左右焦点,P是椭圆是一点,|PF1|=5,则∠F2PF1的大小为( )
| x2 |
| 16 |
| 4y2 |
| 15 |
A、
| ||
B、
| ||
C、
| ||
D、
|
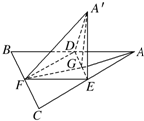 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是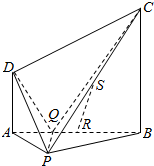 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.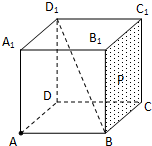 如图,棱长为1的正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持向量
如图,棱长为1的正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持向量