题目内容
已知不等式ax2+bx+c>0的解集是(-2,3),那么cx2+ax+b<0的解集为 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由已知不等式ax2+bx+c>0的解集是(-2,3),得到ax2+bx+c=0的两根为-2,3,得到a,b,c的关系,进一步将cx2+ax+b<0化简解之.
解答:
解:因为不等式ax2+bx+c>0的解集是(-2,3),且a<0,
所以-2+3=-
=1,-2×3=
=-6,
所以b=-a,c=-6a,
所以cx2+ax+b<0为-6ax2+ax-a<0,
所以6x2-x+1<0,解得x∈∅
所以-2+3=-
| b |
| a |
| c |
| a |
所以b=-a,c=-6a,
所以cx2+ax+b<0为-6ax2+ax-a<0,
所以6x2-x+1<0,解得x∈∅
点评:本题考查了一元二次不等式的解集与对应方程的关系;熟练掌握一元二次不等式的解集与相应一元二次方程的实数根的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
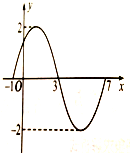 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的一个周期的图象如图.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的一个周期的图象如图.