题目内容
经研究发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:f(t)=
,
(1)求出k的值,并指出讲课开始后多少分钟,学生的注意力最集中?能坚持多久?
(2)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到185,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
|
(1)求出k的值,并指出讲课开始后多少分钟,学生的注意力最集中?能坚持多久?
(2)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到185,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)由分段函数知,求出每一段上的最大值即可判断;
(2)解每一段上f(t)=185的解,从而得到时间段,从而求解.
(2)解每一段上f(t)=185的解,从而得到时间段,从而求解.
解答:
解:(1)当t=20时,f(t)=240,
则有240=20k+400;
解得,k=-8;
当0<t≤10时,f(t)=-t2+26t+80是单调递增的,且f(10)=240;
当10<t≤20时,f(t)=240;
当20<t≤40时,f(t)=-8t+400是单调递减的,且f(20)=240;
故讲课开始后10分钟,学生的注意力最集中,能坚持10分钟;
(2)由f(t)=-t2+26t+80=185解得,t=5或t=21(舍去);
由f(t)=-8t+400=185解得,t=26.875;
故学生的注意力至少达到185的时间有26.875-5=21.875<24;
故老师不能在学生达到所需的状态下讲授完这道题目.
则有240=20k+400;
解得,k=-8;
当0<t≤10时,f(t)=-t2+26t+80是单调递增的,且f(10)=240;
当10<t≤20时,f(t)=240;
当20<t≤40时,f(t)=-8t+400是单调递减的,且f(20)=240;
故讲课开始后10分钟,学生的注意力最集中,能坚持10分钟;
(2)由f(t)=-t2+26t+80=185解得,t=5或t=21(舍去);
由f(t)=-8t+400=185解得,t=26.875;
故学生的注意力至少达到185的时间有26.875-5=21.875<24;
故老师不能在学生达到所需的状态下讲授完这道题目.
点评:本题考查了分段函数在实际问题中的应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
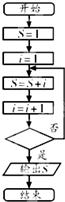 阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )
阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )| A、i>2? | B、i>3? |
| C、i>4? | D、i>5? |
已知直线x-2y-a=0与圆:x2+y2+2x-4y=0相切,则a=( )
| A、0 | B、-10或0 |
| C、-3或0 | D、--10 |
已知抛物线C:y2=8x,过点P(2,0)的直线与抛物线交于A,B两点,O为坐标原点,则
•
的值为( )
| OA |
| OB |
| A、-16 | B、-12 | C、4 | D、0 |