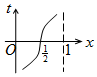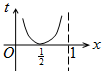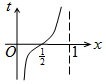题目内容
3.已知集合A={x|x<-2或x>0},B={x|($\frac{1}{3}$)x≥3}(Ⅰ)求A∪B
(Ⅱ)若集合C={x|a<x≤a+1},且A∩C=C,求a的取值范围.
分析 (Ⅰ)求解指数不等式化简集合B,再由并集运算性质求解得答案;
(Ⅱ)由已知得C⊆A,进一步得到a+1<-2或a≥0,求解即可得答案.
解答 解:(Ⅰ)∵${(\frac{1}{3})^x}≥3={(\frac{1}{3})^{-1}}$,且函数$y={(\frac{1}{3})^x}$在R上为减函数,
∴x≤-1.
∴A∪B={x|x<-2或x>0}∪{x|x≤-1}={x|x≤-1或x>0};
(Ⅱ)∵A∩C=C,∴C⊆A,
∴a+1<-2或a≥0,
解得a<-3或a≥0.
点评 本题考查了交集及其运算,考查了集合间的关系,指数不等式的解法,考查运算求解能力、推理论证能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.设集合A={x|2x-2<1},B={x|1-x≥0},则A∩B等于( )
| A. | {x|0<x≤1} | B. | {x|1≤x<2} | C. | {x|x≤1} | D. | {x|0<x<1} |
14.对于常数m、n,“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不必要条件 |
18.矩形ABCD中,AB=2,AD=1,在矩形ABCD的边CD上随机取一点E,记“△AEB的最大边是AB”为事件M,则P(M)等于( )
| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | $\frac{2-\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
8.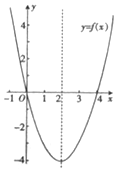 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
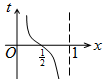
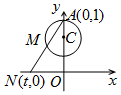 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )