题目内容
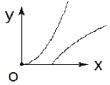
8.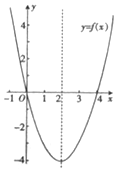 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
分析 利用复合函数的单调性,结合函数的图象判断即可.
解答 解:令u=f(x),函数g(x)=log${\;}_{\frac{1}{2}}$u在(0,+∞)上递减,
结合复合函数的单调性可知:函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间,
就是f(x)的递减区间,且f(x)>0,
故有函数的图象,可知函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为:(-∞,0).
故选:A.
点评 本题考查函数的图象的应用,复合函数的单调性的判断,基本知识的考查.

练习册系列答案
相关题目
19.已知实数x,y满足$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.,z=|{x+2y-4}|$,则z的最大值与最小值之差为( )
| A. | 5 | B. | 1 | C. | 4 | D. | $\frac{7}{3}$ |
13.已知a=0.993,b=log20.6,c=log3π,则( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
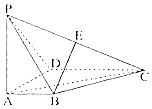 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.