题目内容
18.矩形ABCD中,AB=2,AD=1,在矩形ABCD的边CD上随机取一点E,记“△AEB的最大边是AB”为事件M,则P(M)等于( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | $\frac{2-\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
分析 分别以A、B为圆心,AB为半径作弧,交C、D于P1,P2,△ABE的最大边是AB的概率p=$\frac{{P}_{1}{P}_{2}}{CD}$,由此利用几何概型能求出结果.
解答 解:分别以A、B为圆心,AB为半径作弧,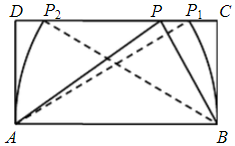 交C、D于P1,P2,
交C、D于P1,P2,
当E在线段P1P2间运动时,能使得△ABE的最大边为AB,
∵在矩形中ABCD中,AB=2,AD=1,
∴AP1=BP2=2,∴CP1=DP2=2-$\sqrt{3}$,
∴P1P2=2-2(2-$\sqrt{3}$)=2$\sqrt{3}$-2,
∴△ABE的最大边是AB的概率:p=$\frac{{P}_{1}{P}_{2}}{CD}$=$\sqrt{3}$-1
故选:B.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意几何概型计算公式的合理运用.

练习册系列答案
相关题目
10.直线x+3y+3=0的斜率是( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | 3 |
7.在直三棱柱ABC-A1B1C1 中,∠ACB=90°,AA1=2,AC=BC=1,记A 1B1 的中点为E,平面C1 EC 与 AB1 C1 的交线为l,则直线l与 AC所成角的余弦值是( )
| A. | $\frac{{\sqrt{6}}}{5}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
8.若a=40.5,b=logπ3,c=logπ4,则( )
| A. | b>c>a | B. | a>b>c | C. | a>c>b | D. | c>a>b |