题目内容
6．
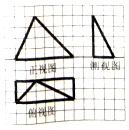我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异”．“势”即是高，“幂”即是面积．意思是说如果两等高的几何体在同高处截得两几何体的截面积相等，那么这两个几何体的体积相等．已知某不规则几何体与如图所对应的几何体满足：“幂势同”，则该不规则几何体的体积为（图中的网格纸中的小正方形的边长为1）（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 20 |
分析 根据三视图，可得该几何体是四棱柱，且该四棱柱的底面是长方形，长为6，宽为2，四棱锥的高为4，求得它的体积，即为所求．
解答 
解：由题意可得，不规则几何体与三视图所对应的几何体的体积相同，
根据三视图，可得该几何体是四棱柱，AH⊥平面ABCD，H∈AB，
且该四棱柱的底面是长方形，长为BC=6，宽为AB=2，四棱锥的高为PH=4，
其中，AH=2，如图所示：
故它的体积为$\frac{1}{3}$•（6•2）•4=16，
故选：C．
点评 本题主要考查祖暅原理，利用三视图求几何体的体积，属于基础题．
练习册系列答案
相关题目
8．下列函数中既是奇函数又是最小正周期为π的函数的是（ ）
| A． | y=|sinx| | B． | $y=cos（{2x+\frac{π}{2}}）$ | C． | y=sin2x+cos2x | D． | y=sinx-cosx |
9．等差数列{an}的前n项和为Sn，S7-S5=24，a3=5，则S7=（ ）
| A． | 25 | B． | 49 | C． | 15 | D． | 40 |
1．下列命题中，错误的是（ ）
| A． | 圆锥所有的轴截面是全等的等腰三角形 | |
| B． | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| C． | 圆锥的轴截面是所有过顶点的界面中面积最大的一个 | |
| D． | 当球心到平面的距离小于球面半径时，球面与平面的交线总是一个圆 |
15．在△ABC中，若（a+b+c）（b+c-a）=3bc，则∠A等于（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}或\frac{2π}{3}$ |