题目内容
1．下列命题中，错误的是（ ）| A． | 圆锥所有的轴截面是全等的等腰三角形 | |
| B． | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| C． | 圆锥的轴截面是所有过顶点的界面中面积最大的一个 | |
| D． | 当球心到平面的距离小于球面半径时，球面与平面的交线总是一个圆 |
分析 根据旋转体的结构特征进行分析判断．
解答 解：对于A，圆锥的轴截面都是以母线为腰，以底面直径为底边的等腰三角形，故A正确；
对于B，圆柱过母线的截面为矩形，一边为圆柱的高，另一边为圆柱底面圆的弦，
∴当另一半为底面直径时截面最大，故B正确；
对于C，设圆锥任意两条母线的夹角为θ，则过此两母线的截面三角形面积为$\frac{1}{2}$l2sinθ，
∴当圆锥轴截面的顶角为钝角，则当θ=$\frac{π}{2}$时，过顶点的截面中面积最大，故C错误；
对于D，球心到平面的距离小于球面半径时，球被平面分成两部分，截面为圆，故D正确．
故选C．
点评 本题考查的知识点是旋转体（圆锥、圆柱、圆台）的结构特征，熟练掌握旋转体的结构特征，是解答本题的关键．
练习册系列答案
相关题目
3．若抛物线y2=2px的焦点与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1的右焦点重合，则p的值为（ ）
| A． | 2$\sqrt{10}$ | B． | 2$\sqrt{2}$ | C． | 4 | D． | 2 |
4．已知$\vec a=（x，4），\vec b=（3，2）$，$\vec a∥\vec b，则x$=（ ）
| A． | -6 | B． | $-\frac{3}{8}$ | C． | 6 | D． | $\frac{3}{8}$ |
9．
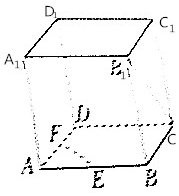如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是AB、AD的中点，则异面直线B1C与EF所成的角的大小为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是AB、AD的中点，则异面直线B1C与EF所成的角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
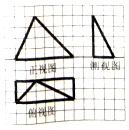我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异”．“势”即是高，“幂”即是面积．意思是说如果两等高的几何体在同高处截得两几何体的截面积相等，那么这两个几何体的体积相等．已知某不规则几何体与如图所对应的几何体满足：“幂势同”，则该不规则几何体的体积为（图中的网格纸中的小正方形的边长为1）（ ）
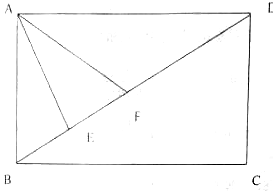小王大学毕业后决定利用所学知识自主创业，在一块矩形的空地上办起了养殖场，如图所示，四边形ABCD为矩形，AB=200米，AD=200$\sqrt{3}$米，现为了养殖需要，在养殖场内要建造蓄水池，小王因地制宜，建造了一个三角形形状的蓄水池，其中顶点分别为A，E，F（E，F两点在线段BD上），且∠EAF=$\frac{π}{6}$，设∠BAE=α．