题目内容
9．等差数列{an}的前n项和为Sn，S7-S5=24，a3=5，则S7=（ ）| A． | 25 | B． | 49 | C． | 15 | D． | 40 |
分析 利用等差数列的通项公式与求和公式即可得出．
解答 解：设等差数列{an}的公差为d．
由等差数列的性质可得：S7-S5=24=a6+a7，a3=5，
∴2a1+11d=24，a1+2d=5，解得a1=1，d=2，
则S7=7+$\frac{7×6}{2}$×2=49．
故选：B．
点评 本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19．
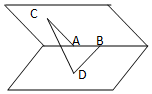如图在一个60°的二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，且AB=AC=1，BD=2，则CD的长为（ ）
如图在一个60°的二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，且AB=AC=1，BD=2，则CD的长为（ ）| A． | 2 | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | 1 |
17．下列4个命题是真命题的个数是（ ）
①“若x2+y2=0，则x、y均为零”的逆命题
②“全等三角形的面积相等”的否命题
③“若A∩B=A，则A⊆B”的逆否命题
④“末位数字不是零的数可被5整除”的逆否命题．
①“若x2+y2=0，则x、y均为零”的逆命题
②“全等三角形的面积相等”的否命题
③“若A∩B=A，则A⊆B”的逆否命题
④“末位数字不是零的数可被5整除”的逆否命题．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．已知$\vec a=（x，4），\vec b=（3，2）$，$\vec a∥\vec b，则x$=（ ）
| A． | -6 | B． | $-\frac{3}{8}$ | C． | 6 | D． | $\frac{3}{8}$ |
9．
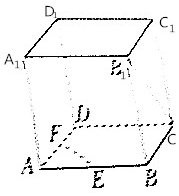如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是AB、AD的中点，则异面直线B1C与EF所成的角的大小为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是AB、AD的中点，则异面直线B1C与EF所成的角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
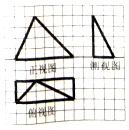我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异”．“势”即是高，“幂”即是面积．意思是说如果两等高的几何体在同高处截得两几何体的截面积相等，那么这两个几何体的体积相等．已知某不规则几何体与如图所对应的几何体满足：“幂势同”，则该不规则几何体的体积为（图中的网格纸中的小正方形的边长为1）（ ）
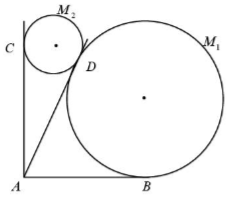某景区欲建两条圆形观景步道M1，M2（宽度忽略不计），如图所示，已知AB⊥AC，AB=AC=AD=60（单位：米），要求圆M与AB，AD分别相切于点B，D，圆M2与AC，AD分别相切于点C，D．