题目内容
14.已知函数f(x)=x+$\frac{4}{x}$.(1)判断函数f(x)的奇偶性,写出判断过程;
(2)证明f(x)在区间(0,2]是单调减函数,在区间[2,+∞)上是单调增函数;
(3)当x∈(0,+∞)时,试求函数f(x)的最大值或最小值.
分析 (1)利用函数奇偶性的定义判断f(-x)与f(x)的关系,在定义域关于原点对称的前提下,相等为偶函数,相反为奇函数;
(2)利用导数与函数单调性的关系,对函数求导,通过导数的符号判断函数的单调性;
(3)利用基本不等式以及函数的单调性求最值.
解答 解:(1)函数f(x)的定义域为{x|x≠0,x∈R}关于原点对称
因为f(-x)=-x-$\frac{4}{x}$=-f(x).
所以f(x)是奇函数.
(2)证明:f'(x)=1-$\frac{4}{{x}^{2}}$,f'(x)在区间(0,2],f'(x)<0,所以在[0,2]是单调减函数,在区间[2,+∞)上f'(x)>0,所以f(x)在[2,+∞)是单调增函数;
(3)当x∈(0,+∞)时,f(x)≥2$\sqrt{x•\frac{4}{x}}$=4,当且仅当x=2时f(x)取最小值4,无最大值.
点评 本题主要考查函数的单调性和奇偶性的判断与证明,同时还考查了利用性质作出函数图象,这类作图不是很准确,但在数形结合中解决问题很有效

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设实数x,y满足约束条件$\left\{\begin{array}{l}{3x-2y+4≥0}\\{x+ay-4≤0}\\{x-y-2≤0}\end{array}\right.$,已知z=2x+y的最大值是7,最小值是-26,则实数a的值为( )
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
17.下列4个命题是真命题的个数是( )
①“若x2+y2=0,则x、y均为零”的逆命题
②“全等三角形的面积相等”的否命题
③“若A∩B=A,则A⊆B”的逆否命题
④“末位数字不是零的数可被5整除”的逆否命题.
①“若x2+y2=0,则x、y均为零”的逆命题
②“全等三角形的面积相等”的否命题
③“若A∩B=A,则A⊆B”的逆否命题
④“末位数字不是零的数可被5整除”的逆否命题.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.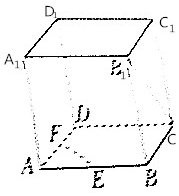 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
4.定义在R上的奇函数f(x)满足f(x)=-f(x+2),且在[1,2]上是减函数,则( )
| A. | $f(\frac{1}{2})<f(-\frac{3}{2})<f(3)$ | B. | $f(3)<f(-\frac{3}{2})<f(\frac{1}{2})$ | C. | $f(\frac{1}{2})<f(3)<f(-\frac{3}{2})$ | D. | $f(3)<f(\frac{1}{2})<f(-\frac{3}{2})$ |
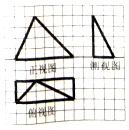 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )
我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )