题目内容
18.已知函数f(x)对任意的实数满足:f(x+3)=-$\frac{1}{f(x)}$,且当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2014)=337.分析 通过f(x+3)=-$\frac{1}{f(x)}$可知函数f(x)是周期T=6的函数,进而可求出f(1)=1,f(2)=2,f(3)=f(-3)=-1,f(4)=f(-2)=0,f(5)=f(-1)=-1,f(6)=f(0)=0,利用2014=335×6+4计算即得结论.
解答 解:因为f(x+3)=-$\frac{1}{f(x)}$,
所以f(x+6)=f(x+3+3)=-$\frac{1}{f(x+3)}$=-$\frac{1}{-\frac{1}{f(x)}}$=f(x),
即函数f(x)是周期T=6的函数,
又因为-3≤x<-1时f(x)=-(x+2)2,当-1≤x<3时f(x)=x,
所以f(1)=1,f(2)=2,f(3)=f(-3)=-1,
f(4)=f(-2)=0,f(5)=f(-1)=-1,f(6)=f(0)=0,
因为2014=335×6+4,且f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1,
所以所求值为335+(1+2-1+0)=337,
故答案为:337.
点评 本题考查求函数的值,考查函数的周期性,考查分段函数,注意解题方法的积累,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.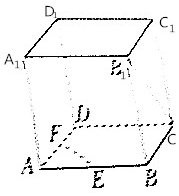 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
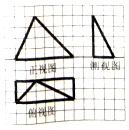 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )
我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理:“幂势既同,则积不容异”.“势”即是高,“幂”即是面积.意思是说如果两等高的几何体在同高处截得两几何体的截面积相等,那么这两个几何体的体积相等.已知某不规则几何体与如图所对应的几何体满足:“幂势同”,则该不规则几何体的体积为(图中的网格纸中的小正方形的边长为1)( )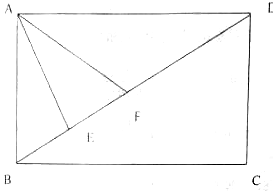 小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.
小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.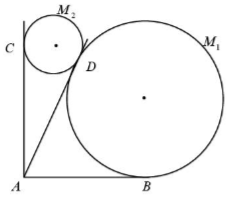 某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.
某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.