题目内容
4.方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆的一个必要不充分条件是( )| A. | m∈(-5,3) | B. | m∈(-3,5) | C. | m∈(-3,1)∪(1,5) | D. | m∈(-5,1)∪(1,3) |
分析 由方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆,可得$\left\{\begin{array}{l}{5-m>0}\\{m+3>0}\\{5-m≠m+3}\end{array}\right.$,解得:m即可判断出结论.
解答 解:由方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆,可得$\left\{\begin{array}{l}{5-m>0}\\{m+3>0}\\{5-m≠m+3}\end{array}\right.$,解得:-3<m<5,且m≠1,
∴方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆的一个必要不充分条件是m∈(-3,5),
故选:B.
点评 本题考查了椭圆的标准方程、充要条件的判定、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
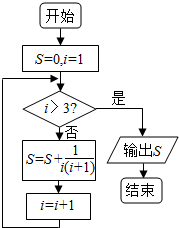

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
9.盒中装有11个乒乓球,其中6个新球,5个旧球,不放回地依次取出2个球,在第一次取出新球的条件下,第二次也取到新球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
14.设点A(2,0),B(4,2),则直线AB的斜率为( )
| A. | 1 | B. | -1 | C. | -2 | D. | 不存在 |