题目内容

9．盒中装有11个乒乓球，其中6个新球，5个旧球，不放回地依次取出2个球，在第一次取出新球的条件下，第二次也取到新球的概率为（　　）
A．$\frac{3}{5}$B．$\frac{1}{6}$C．$\frac{1}{2}$D．$\frac{5}{9}$

分析 在第一次取出新球的条件下，盒子中还有10个球，这10个球中有5个新球和5个旧球，再利用古典概率及其计算公式求得第二次也取到新球的概率

解答 解：在第一次取出新球的条件下，盒子中还有10个球，这10个球中有5个新球和5个旧球，
故第二次也取到新球的概率为$\frac{1}{2}$，
故选C．

点评 本题主要考查古典概率及其计算公式，体现了转化的数学思想，属于基础题

练习册系列答案
相关题目
19．如图的程序框图表示算法的运行结果是（　　）
A．-2B．2C．-1D．1
20．已知抛物线x2=8y上的点P到抛物线的焦点距离为5，则点P的纵坐标为（　　）
A．2B．3C．4D．5
17．已知A，B两地相距100km．按交通法规规定：A，B两地之间的公路上车速要求不低于60km/h且不高于100km/h．假设汽车以xkm/h速度行驶时，每小时耗油量为（$4+\frac{1}{128000}{x^3}-\frac{1}{80}x$）升，汽油的价格是6元/升，司机每小时的工资是24元．
（1）若汽车从A地以64km/h的速度匀速行驶到B地，需耗油多少升？
（2）当汽车以多大的速度匀速行驶时，从A地到B地的总费用最低？
4．方程$\frac{{x}^{2}}{5-m}$+$\frac{{y}^{2}}{m+3}$=1表示椭圆的一个必要不充分条件是（　　）
A．m∈（-5，3）B．m∈（-3，5）C．m∈（-3，1）∪（1，5）D．m∈（-5，1）∪（1，3）
14．执行如图所示的程序框图，若m=3，则输出的结果为（　　）
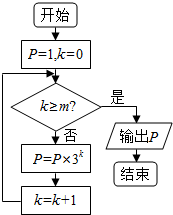
A．3B．27C．81D．729
1．已知数列{an}是各项均为正数的等差数列，首项a1=1，其前n项和为Sn；数列{bn}是等比数列，首项b1=2，且b2S2=16，b3S3=72．
（1）求数列{an}，{bn}的通项公式；
（2）若${c_n}=\frac{S_n}{b_n}$，求数列{cn}的前n项和Tn．
18．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（3，-1），离心率e=$\frac{\sqrt{6}}{3}$．
（1）求椭圆C的方程；
（2）分别过椭圆C的四个顶点作坐标轴的垂线，围成如图所示的矩形，A、B是所围成的矩形在x轴上方的两个顶点．若P、Q是椭圆C上两个动点，直线0P、OQ与椭圆的另一交点分别为P1、Q1，且直线OP、0Q的斜率之积等于直线OA、0B的斜率之积，试问四边形PQP1Q1的面积是否为定值？若为定值，求出其值；若不为定值，说明理由（O为坐标原点）．
19．（1）求证：1+$\frac{1}{{3}^{2}}$+$\frac{1}{{5}^{2}}$+…+$\frac{1}{（2n-1）^{2}}$＞$\frac{7}{6}$-$\frac{1}{2（2n-1）}$（n≥2）
（2）求证：$\frac{1}{4}$+$\frac{1}{16}$+$\frac{1}{36}$+…+$\frac{1}{4{n}^{2}}$＜$\frac{1}{2}$-$\frac{1}{4n}$
（3）求证：$\frac{1}{2}$+$\frac{1•3}{2•4}$+$\frac{1•3•5}{2•4•6}$+…+$\frac{1•3•5…（2n-1）}{2•4•6…2n}$＜$\sqrt{2n+1}$-1
（4）求证：2（$\sqrt{n+1}$-1）＜1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$＜$\sqrt{2}$（$\sqrt{2n+1}$-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网