题目内容
16.已知方程log2x+x-m=0在区间(1,2)上有实根,则实数m的取值范围是(1,3).分析 由方程log2x+x-m=0在区间(1,2)上有实根,则函数f(x)=log2x+x-m在区间(1,2)上有零点,根据函数的单调性和函数的零点存在定理可知f(1)f(2)<0,解得即可.
解答 解:方程log2x+x-m=0在区间(1,2)上有实根,
∴函数f(x)=log2x+x-m在区间(1,2)上有零点,
∵f(x)=log2x+x-m在区间(1,2)上单调递增,
∴f(1)•f(2)<0,
即(1-m)(3-m)<0,
即(m-1)(m-3)<0,
解得1<m<3,
故答案为:(1,3).
点评 本题考查了函数零点的存在定理,属于基础题.

练习册系列答案
相关题目
7.内江市某镇2009年至2015年中,每年的人口总数y(单位:万)的数据如下表:
若t与y之间具有线性相关关系,则其线性回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+$\stackrel{∧}{a}$一定过点( )
| 年 份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 人口总数y | 8 | 8 | 8 | 9 | 9 | 10 | 11 |
| A. | (3,9) | B. | (9,3) | C. | (6,14) | D. | (4,11) |
8. 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )| A. | 24π | B. | $24π+8\sqrt{2}π$ | C. | $24π+4\sqrt{2}π$ | D. | 32π |
5.某企业生产A、B两种产品,现有资源如下:煤360吨,水300吨,电200千瓦.每生产1吨A产品需消耗煤9吨,水3吨,电4千瓦,利润7万元;每生产1吨B产品需消耗煤4吨,水10吨,电5千瓦,利润12万元.
(Ⅰ)根据题目信息填写下表:
(Ⅱ)设分别生产A、B两种产品x吨、y吨,总产值为z万元,请列出x、y满足的不等式组及目标函数.
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
(Ⅰ)根据题目信息填写下表:
| 每吨产品 | 煤(吨) | 水(吨) | 电(千瓦) |
| A | |||
| B |
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
 如图,椭圆的中心在坐标原点,A,B为顶点,F为焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,此类椭圆称为“黄金椭圆”,可推算出“黄金椭圆”的离心率e=$\frac{\sqrt{5}-1}{2}$.
如图,椭圆的中心在坐标原点,A,B为顶点,F为焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,此类椭圆称为“黄金椭圆”,可推算出“黄金椭圆”的离心率e=$\frac{\sqrt{5}-1}{2}$.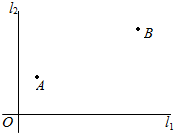 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.