题目内容
曲线C:x=
与直线l:x-y-m=0有两个交点,则实数m的取值范围是 .
| -y2-2y |
考点:直线和圆的方程的应用
专题:直线与圆
分析:作出曲线图象,利用数形结合即可得到结论.
解答:
解:由x=
可知x≥0,
得x2=-y2-2y,
即x2+y2+2y=0,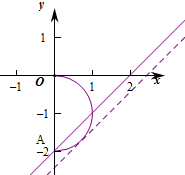
则x2+(y+1)2=1,
作出曲线C:x=
的图象如图:
当直线x-y-m=0经过点A(-2,0)时,直线直线和曲线有两个交点,
此时-2-m=0,交点m=-2,
当直线与曲线相切时,
圆心(-1,0)到直线x-y-m=0的距离d=
=
=1,
即|m+1|=
,
解得m=
-1(舍去)或-
-1,
此时直线和曲线只有一个交点,
故满足条件的m的取值范围为(-
-1,-2],
故答案为:(-
-1,-2]
| -y2-2y |
得x2=-y2-2y,
即x2+y2+2y=0,
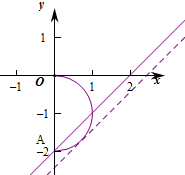
则x2+(y+1)2=1,
作出曲线C:x=
| -y2-2y |
当直线x-y-m=0经过点A(-2,0)时,直线直线和曲线有两个交点,
此时-2-m=0,交点m=-2,
当直线与曲线相切时,
圆心(-1,0)到直线x-y-m=0的距离d=
| |-1-m| | ||
|
| |m+1| | ||
|
即|m+1|=
| 2 |
解得m=
| 2 |
| 2 |
此时直线和曲线只有一个交点,
故满足条件的m的取值范围为(-
| 2 |
故答案为:(-
| 2 |
点评:本题主要考查直线和圆的位置关系的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
从6本不同的数学书和5本不同的英语书中取3本,要求数学书和英语书都要有取到,则不同的取法种数有( )种.
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
函数y=cos2x-sin2x 的一条对称轴为( )
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=-
|
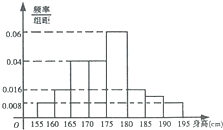 从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图:
从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图: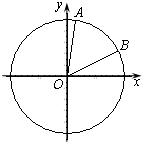 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别交单位圆于A、B两点.已知A、B两点的横坐标分别是
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别交单位圆于A、B两点.已知A、B两点的横坐标分别是