Question

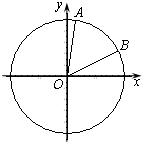如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别交单位圆于A、B两点．已知A、B两点的横坐标分别是

2

10

、

2 5

5

．求tan（α+β）的值=

 

．

Answer 1

考点：两角和与差的正切函数,任意角的三角函数的定义

专题：三角函数的求值

分析：利用cosα=

2

10

，cosβ=

2 5

5

，α、β均为锐角，可求得sinα与sinβ的值，继而可得tanα=7，tanβ=

1

2

，利用两角和的正切即可求得答案．

解答： 解：∵cosα=

2

10

，cosβ=

2 5

5

，α、β均为锐角，
∴sinα=

1-cos2α

=

7 2

10

，sinβ=

1-cos2β

=

5

5

，
∴tanα=7，tanβ=

1

2

，
∴tan（α+β）=

tanα+tanβ

1-tanαtanβ

=

7+ 1 2

1-7× 1 2

=-3．
故答案为：-3．

点评：本题考查任意角的三角函数的定义，考查同角三角函数间的关系式及两角和的正切，属于中档题．