题目内容
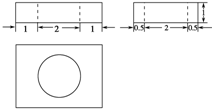
一个几何体的三视图如图所示，求该几何体的表面积和体积．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图，可得：该几何体是一个长方体挖去一个圆柱所得的组合体，分别求出长方体和圆柱的体积，相减可得组合体的体积；分别计算出长方体的表面积，圆柱的底面积和侧面积，用长方体的表面积减两个圆柱的底面面积，再加圆柱的侧面积可得答案．
解答：
解：由已知中的三视图，可得：该几何体是一个长方体挖去一个圆柱所得的组合体，
长方体的长宽高分别为4，3，1，
故长方体的体积为：12，
圆柱的底面半径为1，高为1，
故圆柱的体积为：π，
故组合体的体积为：12-π，
长方体的表面积为：2（1×3+1×4+3×4）=38，
圆柱的底面积为π，
侧面积为：2π，
故几何体的表面积为：38-2π+2π=38．
长方体的长宽高分别为4，3，1，
故长方体的体积为：12，
圆柱的底面半径为1，高为1，
故圆柱的体积为：π，
故组合体的体积为：12-π，
长方体的表面积为：2（1×3+1×4+3×4）=38，
圆柱的底面积为π，
侧面积为：2π，
故几何体的表面积为：38-2π+2π=38．
点评：解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，然后利用几何体的面积及体积公式解决．
练习册系列答案
阅读快车系列答案
相关题目
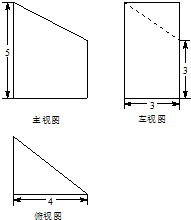
设矩阵M=某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、26 | ||
B、42+3
| ||
| C、62 | ||
D、42-3
|
已知f（x）=cosx•sin2x，下列命题错误的为（ ）
| A、y=f（x）为奇函数 | ||||
B、y=f（x）的图象关于x=
| ||||
C、y=f（x）的最大值为
| ||||
| D、y=f（x）为周期函数 |