Question

设矩阵M=

2 -3 -1 a

，点A（2，1）在矩阵M所对应的线性变换作用下得到点A′（1，-1）．
（Ⅰ）求a的值；
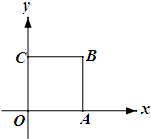
（Ⅱ）如图所示，点A（1，0），点C（0，1），单位正方形OABC在矩阵M所对应的线性变换作用下变成了什么图形？并画出图形．

Answer 1

考点：几种特殊的矩阵变换

专题：矩阵和变换

分析：本题（Ⅰ）由根据矩阵变换，得到矩阵与向量积的等式，利用矩阵与向量的积的法则，得到参数a的方程，解方程求出a的值；（Ⅱ）再利用矩阵与向量的积的计算，得到对应的向量，即得到对应 点的坐标，画图，得到本题结论．

解答： 解：（Ⅰ）由题意：

2 -3 -1 a

2 1

=

1 -1

，
∴-1×2+a=-1，
∴a=1．
（Ⅱ）由（Ⅰ）知：M=

2 -3 -1 1

，
∵

2 -3 -1 1

1 0

=

2 -1

，
∴点A（1，0）在矩阵M所对应的线性变换作用下的点A′（2，-1）．
同理，点B（1，1）在矩阵M所对应的线性变换作用下的点B′（-1，0），
点C（0，1）在矩阵M所对应的线性变换作用下的点C′（-3，1），
因此单位正方形OABC在矩阵M所对应的线性变换作用下变成了平行四边形OA′B′C′．
如图：

点评：本题考查了矩阵与向量的积的运算，本题难度不大，属于基础题．