题目内容
设函数f(x)=sin(-2x+∅)(0<∅<π),y=f(x)图象的一条对称轴是直线x=
,则∅= .
| π |
| 6 |
考点:正弦函数的对称性
专题:三角函数的图像与性质
分析:由题意可得-2×
+∅=kπ+
,k∈z,再结合0<∅<π,可得∅的值.
| π |
| 6 |
| π |
| 2 |
解答:
解:由题意可得-2×
+∅=kπ+
,k∈z,即∅=kπ+
,k∈z.
再结合0<∅<π,可得∅=
,
故答案为:
.
| π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
再结合0<∅<π,可得∅=
| 5π |
| 6 |
故答案为:
| 5π |
| 6 |
点评:本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
已知x,y如下表所示,若x和y线性相关,
且线性回归直线方程是
=bx+2.4,则b=( )
| x | 1 | 2 | 3 | 4 | 5 |
| y[ | 2.9 | 3.7 | 4.5 | 5.3 | 6.1 |
| ? |
| y |
| A、0.7 | B、0.8 |
| C、0.9 | D、1 |
已知集合D={x|
>0},若a,b∈D且
+
=
,则9a•3b的最小值为( )
| 24-x |
| x-9 |
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 12 |
| A、27 |
| B、327 |
| C、54 |
| D、354 |
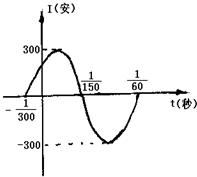 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.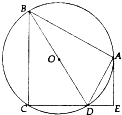 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.