题目内容
不等式x4+2x2+a2-a-2≥0对x∈R恒成立，则a的取值范围 ．
考点：一元二次不等式的解法,函数恒成立问题
专题：不等式的解法及应用
分析：不等式x4+2x2+a2-a-2≥0对x∈R恒成立，也即不等式x4+2x2≥-（a2-a-2）对x∈R恒成立，
故只需使（x4+2x2）min≥-（a2-a-2）对x∈R恒成立，求出x4+2x2的最小值，代入的关于a的不等式，解此不等式，求得a的取值范围．
故只需使（x4+2x2）min≥-（a2-a-2）对x∈R恒成立，求出x4+2x2的最小值，代入的关于a的不等式，解此不等式，求得a的取值范围．
解答：
解：不等式x4+2x2+a2-a-2≥0对x∈R恒成立，也即不等式x4+2x2≥-（a2-a-2）对x∈R恒成立，
∴只需使（x4+2x2）min≥-（a2-a-2）对x∈R恒成立，
∵x4+2x2=（x2+1）2-1，而x2≥0，
∴当x2=0时，x4+2x2取最小值，即（x4+2x2）min=0
∴0≥-（a2-a-2）
∴a2-a-2≥0
解得a≤-1或a≥2
故答案为：（-∞，-1]∪[2，+∞）
∴只需使（x4+2x2）min≥-（a2-a-2）对x∈R恒成立，
∵x4+2x2=（x2+1）2-1，而x2≥0，
∴当x2=0时，x4+2x2取最小值，即（x4+2x2）min=0
∴0≥-（a2-a-2）
∴a2-a-2≥0
解得a≤-1或a≥2
故答案为：（-∞，-1]∪[2，+∞）
点评：本题主要考查二次不等式的解法，函数的恒成立问题，属于中档题．
练习册系列答案
相关题目
函数y=
sinx(
＜x＜
)的值域是（ ）
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、（0，
| ||||
B、(
| ||||
C、(0，
| ||||
| D、（0，1） |
已知在区间[-1，1]上随机地取一个数x，则-π（x2-1）的值介于
到π之间的概率为（ ）
| 8π |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
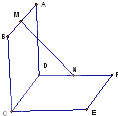如图，已知两个正方形ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点．若平面ABCD⊥平面DCEF，求直线MN与平面DCEF所成角的正弦值．