题目内容
已知y=y1+y2,y1与
成正比例,y2与x+3成反比例,并且x=0时,y=4,x=3时y=5,求y与x之间的函数关系式.
| x+1 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:首先,设y1=k
,y2=
,然后,将x=0时,y=4,x=3时y=5,代人求解待定系数的值即可.
| x+1 |
| m |
| x+3 |
解答:
解:∵y1与
成正比例,y2与x+3成反比例,
∴设y1=k
,y2=
,
∴y=y1+y2=k
+
,
∵x=0时,y=4,x=3时y=5,
∴
,
∴
,
∴y=2
+
.
∴y与x之间的函数关系式y=2
+
.
| x+1 |
∴设y1=k
| x+1 |
| m |
| x+3 |
∴y=y1+y2=k
| x+1 |
| m |
| x+3 |
∵x=0时,y=4,x=3时y=5,
∴
|
∴
|
∴y=2
| x+1 |
| 6 |
| x+3 |
∴y与x之间的函数关系式y=2
| x+1 |
| 6 |
| x+3 |
点评:本题重点考查了函数关系式的求解方法、待定系数法在求解中应用等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知双曲线x2-
=1的两个焦点分别为F1、F2,点P为双曲线上一点,且∠F1PF2=90°,则△F1PF2的周长等于( )
| y2 |
| 3 |
| A、6 | ||
| B、8 | ||
C、4+2
| ||
D、2+2
|
“关于x的方程x4+ax2+b=0有解”是“关于x的方程x2+ax+b=0”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
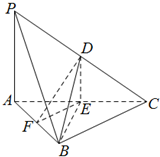 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.