题目内容
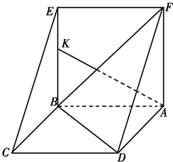 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.(Ⅰ)求证:CE∥平面ADF;
(Ⅱ)若K为线段BE上异于B,E的点,CE=2
| 2 |
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)利用已知条件证明CE∥DF,通过直线与平面平行的判定定理证明CE∥平面ADF.
(Ⅱ)说明BE⊥平面ABCD.以B为原点,
、
、
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,求出相关点的坐标,平面BDF的一个法向量.
=(0,-2,m),利用sinφ=|
|=
,利用φ的范围,推出
≤sinφ≤
,推出{
,解得m的范围,即BK的取值范围.
(Ⅱ)说明BE⊥平面ABCD.以B为原点,
| BC |
| BA |
| BE |
| AK |
| ||||
|
|
| |2+m| | ||||
|
| 1 |
| 2 |
| ||
| 2 |
|
解答:
解:(Ⅰ)证明:正方形ABCD中,CD
BA,正方形ABEF中,EF
BA.…(2分)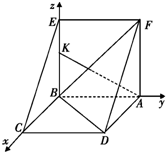
∴EF
CD,∴四边形EFDC为平行四边形,∴CE∥DF.…(3分)
又DF?平面ADF,CE?平面ADF,∴CE∥平面ADF. …(5分)
(Ⅱ)解:∵BE=BC=2,CE=2
,∴CE2=BC2+BE2.
∴△BCE为直角三角形,BE⊥BC,…(6分)
又BE⊥BA,BC∩BA=B,BC、BA?平面ABCD,∴BE⊥平面ABCD. …(7分)
以B为原点,
、
、
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,则B(0,0,0),F(0,2,2),A(0,2,0),
=(2,2,0),
=(0,2,2).
设K(0,0,m),平面BDF的一个法向量为
=(x,y,z).
由
•
=0,
•
=0,得
可取
=(1,-1,1),…(9分)
又
=(0,-2,m),于是sinφ=|
|=
,
∵30°≤φ≤45°,∴
≤sinφ≤
,即{
…(11分)
结合0<m<2,解得0<m≤4-2
,即BK的取值范围为(0,4-
].…(13分)
| ∥ |
. |
| ∥ |
. |

∴EF
| ∥ |
. |
又DF?平面ADF,CE?平面ADF,∴CE∥平面ADF. …(5分)
(Ⅱ)解:∵BE=BC=2,CE=2
| 2 |
∴△BCE为直角三角形,BE⊥BC,…(6分)
又BE⊥BA,BC∩BA=B,BC、BA?平面ABCD,∴BE⊥平面ABCD. …(7分)
以B为原点,
| BC |
| BA |
| BE |
| BD |
| BF |
设K(0,0,m),平面BDF的一个法向量为
| n |
由
| n |
| BD |
| n |
| BF |
|
| n |
又
| AK |
| ||||
|
|
| |2+m| | ||||
|
∵30°≤φ≤45°,∴
| 1 |
| 2 |
| ||
| 2 |
|
结合0<m<2,解得0<m≤4-2
| 3 |
| 3 |
点评:本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、抽象概括能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知△ABC的三边分别为4,5,6,则△ABC的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
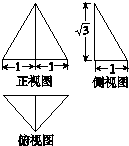 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为