题目内容
已知△ABC的三边分别为4,5,6,则△ABC的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理的应用,三角形中的几何计算
专题:解三角形
分析:根据余弦定理先求出其中一个角的余弦值,然后求出对应的正弦值,利用三角形的面积公式即可得到结论.
解答:
解:∵△ABC的三边长a=4,b=5,c=6,
∴由余弦定理得cosC=
=
,
∴sinC=
=
=
∴三角形的面积为S=
absinC=
×4×5×
=
.
故选:B.
∴由余弦定理得cosC=
| 42+52-62 |
| 2×4×5 |
| 1 |
| 8 |
∴sinC=
1-(
|
| ||
| 8 |
3
| ||
| 8 |
∴三角形的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
15
| ||
| 4 |
故选:B.
点评:本题主要考查了三角形的面积的计算,利用余弦定理和正弦定理求出其中一个角的正弦值是解决本题的关键.

练习册系列答案
相关题目
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线
-y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
| x2 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=
x3-
x2+
x+1在x=1处的切线的倾斜角为α,则
的值是( )
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| cos2α |
| sin2α-cos2α |
A、
| ||
B、
| ||
C、-
| ||
D、-
|

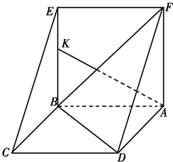 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.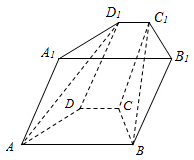 如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.
如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.