题目内容

已知函数f（x）=
1
4
x2+cosx，f′（x）是函数f（x）的导函数，则f′（x）的图象大致是（　　）
A、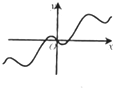
B、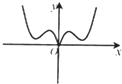
C、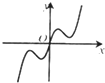
D、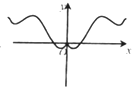
考点：函数的图象
专题：函数的性质及应用
分析：由于f（x）=x+cosx，得f′（x）=
1
2
x-sinx，由奇函数的定义得函数f′（x）为奇函数，其图象关于原点对称，排除BD，取x=
π
2
代入f′（
π
2
）=
π
4
-sin
π
2
=
π
4
-1＜0，排除C，只有A适合．
解答： 解：由于f（x）=x+cosx，
∴f′（x）=
1
2
x-sinx，
∴f′（-x）=-f′（x），故f′（x）为奇函数，其图象关于原点对称，排除BD，
又当x=
π
2
时，f′（
π
2
）=
π
4
-sin
π
2
=
π
4
-1＜0，排除C，只有A适合，
故选：A．
点评：本题考查函数的图象，考查同学们对函数基础知识的把握程度以及数形结合的思维能力，同时考查导数的计算，属于中档题．
练习册系列答案
相关题目
平面向量的集合A 到A的映射f（
x
）=
x
-2（
x
•
a
）
a
，其中
a
为常向量．若映射f满足f（
x
）•f（
y
）=
x
•
y
对任意的
x
，
y
∈A恒成立，则
a
的坐标不可能是（　　）
A、（0，0）
B、（
2
4
，
2
4
）
C、（
2
2
，
2
2
）
D、（-
1
2
，
3
2
）
设无穷数列{an}，如果存在常数A，对于任意给定的正数?（无论多小），总存在正整数N，使得n＞N时，恒有|an-A|＜?成立，就称数列{an}的极限为A，则四个无穷数列：
①{（-1）n×2}；
②{
1
1×3
+
1
3×5
+
1
5×7
+…+
1
(2n-1)(2n+1)
}；
③{1+
1
2
+
1
22
+
1
23
+…+
1
2n-1
}；
④{1×2+2×22+3×23+…+n×2n}，
其极限为2共有（　　）
A、4个B、3个C、2个D、1个
已知数列{an}中，a1=1，an+1=
1
3
an+n，n为奇数
an-3n，n为偶数

（I）求证：数列{a2n-
3
2
}是等比数列；
（II）若Sn是数列{an}的前n项和，求满足Sn＞0的所有正整数n．
给定区间D，对于函数d=2及任意的f（x）、g（x）（其中x1＞x2），若不等式f（x1）-g（x1）＞f（x2）-g（x2）恒成立，则称函数f（x）是相对于函数g（x）在区间上的“渐进函数”，已知=f（x）=x2+2ax是相对于函数g（x）=x+3在区间[a，a+2]上的“渐进函数”，则实数l的取值范围是（　　）
A、a＞
1
4
B、a≤
1
4
C、a≥-
3
4
D、a≤-
3
4
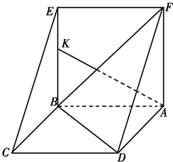如图，边长为2的正方形ABCD绕AB边所在直线旋转一定的角度（小于180°）到ABEF的位置．
（Ⅰ）求证：CE∥平面ADF；
（Ⅱ）若K为线段BE上异于B，E的点，CE=2
2
．设直线AK与平面BDF所成角为φ，当30°≤φ≤45°时，求BK的取值范围．
已知函数f（x）=（ax2+2x-a）ex，g（x）=
1
2
f（lnx），其中a∈R，e=2.71828…为自然对数的底数．
（Ⅰ）若函数y=f（x）的图象在点M（2，f（2））处的切线过坐标原点，求实数a的值；
（Ⅱ）若f（x）在[-1，1]上为单调递增函数，求实数a的取值范围．
（Ⅲ）当a=0时，对于满足0＜x1＜x2的两个实数x1，x2，若存在x0＞0，使得g′（x0）=
g(x1)-g(x2)
x1-x2
成立，试比较x0与x1的大小．
如图，在△ABC中，若AB=1，AC=3，
AB
•
AC
=
3
2
，则BC=
 
设数列{an}的前n项和为Sn，S1=2，当n≥2时，Sn=3Sn-1则数列{an}的通项公式为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网