题目内容
若函数f(x)=2x-
在定义域(0,1]上是减函数,求实数a的取值范围 .
| a |
| x |
考点:函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:求出函数f(x)=2x-
的导数f′(x),由已知可得f′(x)≤0在(0,1]恒成立,运用参数分离,求出右边的最小值即可.
| a |
| x |
解答:
解:函数f(x)=2x-
的导数f′(x)=2+
,
f(x)在定义域(0,1]上是减函数,
则有2+
≤0在(0,1]恒成立,
则a≤-2x2在(0,1]恒成立,
由于-2x2在(0,1]递减,则最小值为-2.
则a≤-2.
故答案为:(-∞,-2]
| a |
| x |
| a |
| x2 |
f(x)在定义域(0,1]上是减函数,
则有2+
| a |
| x2 |
则a≤-2x2在(0,1]恒成立,
由于-2x2在(0,1]递减,则最小值为-2.
则a≤-2.
故答案为:(-∞,-2]
点评:本题考查已知函数的单调性求参数的范围,注意运用导数求解,同时也可以运用单调性的定义,考查运算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在△ABC中,AC=2,BC=1,cosC=
,则△ABC的面积为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
在△ABC中,若a=5,b=4,A=60°,则此三角形有( )
| A、一解 | B、两解 |
| C、无解 | D、解的个数不确定 |
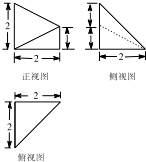 某几何体的三视图如图所示,该几何体的表面积是
某几何体的三视图如图所示,该几何体的表面积是