题目内容
f(x)=
+lg(2x+1)的定义域是( )
| 3x2 | ||
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-∞,-
|
考点:函数的定义域及其求法,对数函数的定义域
专题:函数的性质及应用
分析:根据函数f(x)的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答:
解:∵函数f(x)=
+lg(2x+1),
∴
,
解得-
<x<
;
∴函数的定义域是(-
,
).
故选:C.
| 3x2 | ||
|
∴
|
解得-
| 1 |
| 2 |
| 1 |
| 2 |
∴函数的定义域是(-
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查了求函数定义域的问题,解题时应根据函数的解析式进行解答,是基础题.

练习册系列答案
相关题目
在△ABC中,AC=2,BC=1,cosC=
,则△ABC的面积为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
对任意的正数s,t,有下列4个关系式:
①f(s+t)=f(s)+f(t);
②f(s+t)=f(s)f(t);
③f(st)=f(s)+f(t);
④f(st)=f(s)f(t).
则下列函数中,不满足任何一个关系式的是( )
①f(s+t)=f(s)+f(t);
②f(s+t)=f(s)f(t);
③f(st)=f(s)+f(t);
④f(st)=f(s)f(t).
则下列函数中,不满足任何一个关系式的是( )
| A、y=kx+b(kb≠0) |
| B、y=x2 |
| C、y=ax(a>0,且a≠1) |
| D、y=logax(a>0,且a≠1) |
在△ABC中,若a=5,b=4,A=60°,则此三角形有( )
| A、一解 | B、两解 |
| C、无解 | D、解的个数不确定 |
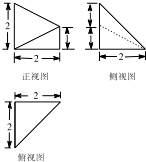 某几何体的三视图如图所示,该几何体的表面积是
某几何体的三视图如图所示,该几何体的表面积是 某家具生产厂需要在一个半径为1的圆形木料中依照图纸方式切割出如图十字图形,其中∠AEF=θ(θ为变量),AB=HG=x,AF=y.
某家具生产厂需要在一个半径为1的圆形木料中依照图纸方式切割出如图十字图形,其中∠AEF=θ(θ为变量),AB=HG=x,AF=y.