题目内容
若复数z满足(1+2i)z=3-4i,则|z|等于 .
考点:复数求模
专题:数系的扩充和复数
分析:根据复数的代数运算以及模长公式,进行计算即可.
解答:
解:∵复数z满足(1+2i)z=3-4i,
∴z=
,
∴|z|=|
|
=
=
=
.
故答案为:
.
∴z=
| 3-4i |
| 1+2i |
∴|z|=|
| 3-4i |
| 1+2i |
=
| |3-4i| |
| |1+2i| |
=
| 5 | ||
|
=
| 5 |
故答案为:
| 5 |
点评:本题考查了复数的代数运算以及求复数模长的应用问题,是基础题目.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
将函数y=sin(2x+
)的图象沿x轴向左平移m(m>0)个单位后,得到一个奇函数的图象,则m的最小值为( )
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若球的半径扩大到原来的2倍,那么体积扩大到原来的( )
| A、64倍 | B、16倍 |
| C、8倍 | D、4倍 |
“a=1”是“a2=1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
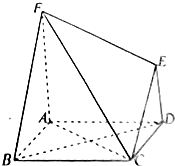 在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE
在如图所示的多面体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,DE⊥平面ABCD,且AF=2DE