题目内容
将函数y=sin（2x+
）的图象沿x轴向左平移m（m＞0）个单位后，得到一个奇函数的图象，则m的最小值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：计算题,三角函数的图像与性质
分析：根据图象变换规律，把函数y=sin（2x+
）的图象向右平移m个单位得到函数y=sin[2（x+m）+
]；要使所得到的图象对应的函数为奇函数，只需2m+
=kπ，从而求得m的最小值．
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
解答：
解：y=sin（2x+
）的图象向右平移m个单位长度后得到y=sin[2（x+m）+
]，
∵y=sin[2（x+m）+
]为奇函数，
∴sin（2m+
）=0，
∴2m+
=kπ，k∈Z，即有m=
-
，k∈Z，
∴正数m最小值为：
．
故选：A．
| π |
| 8 |
| π |
| 8 |
∵y=sin[2（x+m）+
| π |
| 8 |
∴sin（2m+
| π |
| 8 |
∴2m+
| π |
| 8 |
| kπ |
| 2 |
| π |
| 16 |
∴正数m最小值为：
| 7π |
| 16 |
故选：A．
点评：本题考查了三角函数的图象变换以及三角函数的奇偶性，属于基础题型．解决本题的关键在于得到平移后的函数解析式．
练习册系列答案
相关题目
图中的程序框图所描述的算法称为欧几里得辗转相除法． 若输入m=209，n=121，则输出m=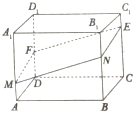
如图4所示，已知直四棱柱ABCD-A1B1C1D1的底面是棱形，其边长为4，∠BAD=60°，点M，N，E分别在棱AA1，BB1，CC1上，过M，N，E的面与棱DD1交于F，AM=2，BN=4，CE=5．求：化简sin
cos
-cos
sin
的值为（ ）
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| A、0 | ||||
| B、1 | ||||
C、
| ||||
D、
|
若函数f（x）=
（a＞0，且a≠1）在（0，+∞）上是增函数，则a的范围是（ ）
|
A、（0，
| ||
| B、（0，1） | ||
C、（0，
| ||
D、[
|