题目内容
在等比数列{an}中,a1=2,前n项的和为Sn,若数列{an+1}也是等比数列,求an和Sn.
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:根据数列{an}为等比数列可设出an的通项公式,因数列{an+1}也是等比数列,根据等比数列的性质求得公比q,进而根据等比数列的求和公式求出sn.
解答:
解:∵数列{an}为等比数列,则an=2qn-1,
又数列{an+1}也是等比数列,
则(an+1+1)2=(an+1)(an+2+1),
∴an+12+2an+1=anan+2+an+an+2,
∴an+an+2=2an+1,
∴an(1+q2-2q)=0,
∴q=1.
即an=2,
∴sn=2n.
又数列{an+1}也是等比数列,
则(an+1+1)2=(an+1)(an+2+1),
∴an+12+2an+1=anan+2+an+an+2,
∴an+an+2=2an+1,
∴an(1+q2-2q)=0,
∴q=1.
即an=2,
∴sn=2n.
点评:本题考查了等比数列的定义和求和公式,着重考查了运算能力,是基础题.

练习册系列答案
相关题目
化简sin
cos
-cos
sin
的值为( )
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| A、0 | ||||
| B、1 | ||||
C、
| ||||
D、
|
函数f(x)=2x+3x-7的零点所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
若函数f(x)=
(a>0,且a≠1)在(0,+∞)上是增函数,则a的范围是( )
|
A、(0,
| ||
| B、(0,1) | ||
C、(0,
| ||
D、[
|
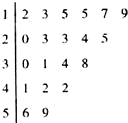 为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为
为了解某校教师使用多媒体辅助教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了解他们上学期使用多媒体辅助教学的次数,结果用茎叶图表示(如图),据此可估计该校上学期200名教师中,使用多媒体辅助教学不少于30次的教师人数为