题目内容
在平面内,若三角形的面积为S,周长为C,则此三角形的内切圆的半径r=
;在空间中,三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,且PA=PB=PC=1,利用类比推理的方法,求得此三棱锥P-ABC的内切球(球面与三棱锥的各个面均相切)的半径R= .
| 2S |
| C |
考点:类比推理
专题:推理和证明
分析:由平面内三角形的内切圆的半径r=
类比推理得出空间中三棱锥内切球的半径R=
;代入计算即可.
| 2S |
| C |
| 3V |
| s1+s2+s3+s4 |
解答:
解:∵平面内,三角形的面积为S,周长为C,则此三角形的内切圆的半径r=
,如图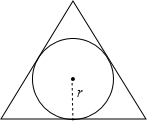 ;
;
设三角形的边长为a、b、c,则三角形的面积为
ra+
rb+
rc=
r(a+b+c)=
rC=S,
∴内切圆半径r=
;
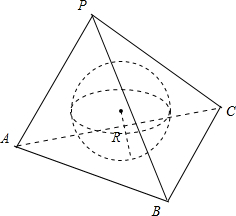
由此类推,设三棱锥的四个面的面积为s1、s2、s3、s4,内切球半径为R,如图;
则四棱锥的体积为
Rs1+
Rs2+
Rs3+
Rs4=
R(s1+s2+s3+s4)=V,
∴内切球半径R=
=
=
;
故答案为:
.
| 2S |
| C |
 ;
;设三角形的边长为a、b、c,则三角形的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴内切圆半径r=
| 2S |
| C |
由此类推,设三棱锥的四个面的面积为s1、s2、s3、s4,内切球半径为R,如图;
则四棱锥的体积为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴内切球半径R=
| 3V |
| s1+s2+s3+s4 |
3×
| ||||||||
3×
|
3-
| ||
| 6 |

故答案为:
3-
| ||
| 6 |
点评:本题考查了用类比推理的方法求三棱锥内切球半径的问题,是基础题.

练习册系列答案
相关题目
已知全集为R,集合A={x|
≤1},B={x|-1≤x≤3},则A∩∁RB=( )
| 1 |
| x |
| A、(-1,3) |
| B、[-1,0]∪[1,3] |
| C、(-∞,-1)∪(3,+∞) |
| D、[1,3] |
已知集合M={x|
≥0,x∈R},集合N={x||x|≤1,x∈R},则M∩N=( )
| x |
| x+1 |
| A、{x|0<x≤1} |
| B、{x|0≤x≤1} |
| C、{x1-1<x≤1} |
| D、{x1-1<x≤1} |
在同一直角坐标系中,经过伸缩变换
后,曲线C变为曲线x′2+y′2=1,则曲线C的方程为( )
|
| A、25x2+9y2=1 | ||||
| B、9x2+25y2=1 | ||||
| C、25x+9y=1 | ||||
D、
|
直线y=x-1被椭圆x2+4y2=4截得的弦长为( )
A、
| ||||
B、
| ||||
C、3或
| ||||
D、
|